Réseau de neurones - Partie 1 : un neurone très simple #
Le problème #
Nous allons construire un simple réseau de neurone pour résoudre un problème.
Nous en profiterons pour expliquer le fonctionnement d’un réseau de neurones.
Voici notre problème de départ.
On dispose des entrées (colonnes 2, 3 et 4) qui génèrent une sortie (colonne 5).
Par exemple, si les entrées sont [0, 0, 1] la sortie est 0. etc.
| Input 1 | Input 2 | Input 3 | Outputs | |
|---|---|---|---|---|
| Exemple 1 | 0 | 0 | 1 | 0 |
| Exemple 2 | 1 | 1 | 1 | 1 |
| Exemple 3 | 1 | 0 | 1 | 1 |
| Exemple 4 | 0 | 1 | 1 | 0 |
On aimerait créer un programme qui apprenne automatiquement à prédire une sortie pour une nouvelle entrée.
| Input 1 | Input 2 | Input 3 | Outputs | |
|---|---|---|---|---|
| Nouvelle situation | 1 | 0 | 0 | ? |
Quelle devrait-être la nouvelle sortie ?
Prenez le temps d’examiner les entrées pour essayer de deviner la solution…
Certains l’ont sûrement deviné, la sortie devrait être 1.
La solution est presque évidente :
- si la première entrée est
0, la sortie est0, - si la première entrée est
1, la sortie est1.
C’est ce qu’on aimerait que fasse notre réseau de neurones : on voudrait qu’il
prédise 1 dans ce cas.
Perceptron #
Notre réseau de neurones est très simple, il n’a pas de couche cachée. C’est ce qu’on appelle un perceptron.
Il contient 4 parties :
- Les entrées, ce sont nos données,
- Les synapses font le lien entre les entrées et le neurone,
- Le neurone lui même qui fait les calculs,
- La sortie, qui est la réponse du neurone aux entrées qu’on lui fournit.
entrées et sortie #
On peut lui donner les valeurs qu’on veut,
-
d’abord les données en entrée : $x_1, x_2, x_3$
-
Ensuite les poids (weights) des synapses $w_1, w_2, w_3$.
Sans entrer dans le détail maintenant, les poids sont les données les plus importantes. Ils sont générés par le programme lui même. Un poids très grand (positif) ou très faible (négatif) aura une grande influence sur le neurone.
-
Ces données (entrées et poids) vont dans le neurone (on détaillera son fonctionnement plus tard) et il calcule la sortie $ŷ$.
Les poids #
Dans un premier temps les poids sont générés aléatoirement, ils n’ont donc aucune chance de convenir !
Notre algorithme va simplement améliorer les poids jusqu’à ce qu’il obtienne le meilleur résultat possible pour nos données.
L’algorithme que nous allons employer s’appelle back propagation, en particulier propagation par descente de gradient.
Il existe de nombreux algorithmes qui reposent sur le même principe.
Le neurone #
Dans le neurone, on réalise un “simple” calcul.
$$\widehat{y} = \phi \left( \sum_{i=1}^3 x_i w_i\right)$$
En détail, partons de l’intérieur du calcul :
-
$$\sum_{i=1}^3 x_i w_i$$
C’est-à-dire : $x_1 \times w_1 + x_2 \times w_2 + x_3 \times w_3$.
On multiplie chaque entrée par son poids et on fait la somme.
La notation symbolique $\sum$ permet d’écrire la formule de façon condensée et sera pratique si le neurone contient un grand nombre d’entrées.
-
$\phi ( \ldots)$ : on applique la fonction $\phi$ au résultat qu’on vient d’obtenir. $\phi$ est la fonction de normalisation.
La fonction de normalisation sigmoid. #
Une fonction de normalisation doit prendre en entrée un nombre réel et renvoyer en sortie un nombre entre $0$ et $1$. Elle doit respecter d’autres critères : être croissante, avoir une certaine allure graphique etc.
Parmi ces fonctions, il en existe une très pratique : la fonction sigmoid.
Son intérêt réside dans une équation dont on parlera plus tard. Disons simplement que sa dérivée se calcule très facilement. Et, justement, on aura besoin de calculer sa dérivée pour ajuster les poids.
On utilisera donc $\phi(x) = \dfrac{1}{1+e^{-x}}$, la fonction sigmoid :

On peut vérifier qu’elle est bien définie sur $]-\infty;+\infty[$, strictement croissante et à image dans $]-1;1[$.
Remarquez bien que $-1$ et $1$ ne sont pas atteints. C’est généralement le cas des fonctions de normalisation et cela aura une conséquence sur nos résultats finaux.
Donc, en résumé :
- On prend les entrées,
- On multiplie chaque entrée par son poids,
- On fait la somme de tout ce beau monde,
- On applique sigmoid au résultat.
On en sait assez pour commencer à développer notre programme. Attaquons !
Première partie du développement #
Dans un premier temps nous allons importer numpy qui nous évitera d’avoir à
implémenter nous même le détail des calculs. Ils ne posent pas vraiment de
problèmes mais :
- ce n’est pas l’objet de ce tutoriel,
numpyest LA bibliothèque de calcul numérique en Python et tout les scientifiques s’en servent,- notre programme sera plus rapide si on l’utilise que si on implémente nous même les calculs
import numpy as np
Ensuite on crée la fonction sigmoid. numpy comporte les fonctions usuelles
des mathématiques dont la fonction exponentielle.
def sigmoid(x):
'''
Sigmoid : normalise les entrées
@param x: (float)
@return: float
'''
return 1 / (1 + np.exp(-x))
Maintenant on ajoute notre exemple d’entraînement.
Les entrées sont données par un tableau à deux dimensions comportant 4 lignes et 3 colonnes. Chaque ligne est un exemple d’entraînement et chaque colonne est une entrée.
Pour cela on utilise la méthode np.array qui permet de définir et de manipuler
facilement ce type de données :
# Les données en entrée
training_inputs = np.array([[0, 0, 1],
[1, 1, 1],
[1, 0, 1],
[0, 1, 1]])
La sortie est aussi un vecteur comportant 4 lignes. Par convention on la donne
en ligne et on transpose cette ligne. C’est à dire qu’on la tourne pour en
faire une colonne avec la méthode .T de numpy :
# Les données en sortie
training_outputs = np.array([[0, 1, 1, 0]]).T
Maintenant on peut initialiser nos poids. Ils sont d’abord choisis aléatoirement entre $-1$ et $1$. Afin de d’obtenir tous les mêmes résultats et de pouvoir retrouver facilement une erreur on donne au générateur aléatoire une racine (seed).
# La racine du générateur aléatoire pour qu'on puisse comparer nos résultats
np.random.seed(1)
Le générateur de nombre aléatoires renvoit un nombre entre $0$ et $1$, on applique une transformation affine pour se ramener entre $-1$ et $1$ :
$$\text{Si } x \in ]0;1[ \text{, alors } 2x - 1 \in ]-1;1[$$
# On crée un vecteur de poids aléatoires centrés sur 0
synaptic_weights = 2 * np.random.random((3, 1)) - 1
print('Poids synaptiques aléatoires: ')
print(synaptic_weights)
Les paramètres 3, 1 nous donnent un tableau à 3 lignes et 1 colonne comme
souhaité.
On affiche les poids initiaux pour conserver une trace lors de l’exécution.
Abordons la boucle principale.
Dans un premier temps, une seule itération ! Nous n’avons pas abordé la partie apprentissage et on ne peut que calculer le résultat.
# On tière 1 fois : pour l'instant !
for iteration in range(1):
# On défini la couche d'entrée
input_layer = training_inputs
# On normalise le produit des entrées par les poids synaptiques
outputs = sigmoid(np.dot(input_layer, synaptic_weights))
print("Sorties après l'entraînement")
print(outputs)
À chaque tour de la boucle les poids seront redéfinis. Il n’est pas utile de redéfinir la couche d’entrée car nous n’avons qu’un neurone mais cela sera commode pour la suite.
Détaillons la ligne :
outputs = sigmoid(np.dot(input_layer, synaptic_weights))
np.dot( ) est un produit scalaire, c’est ce qu’on fait dans le calcul :
$$x_1 \times w_1 + x_2 \times w_2 + x_3 \times w_3$$
On fait bien le produit scalaire $\overrightarrow{X}\cdot \overrightarrow{W}$ avec $\overrightarrow{X} = (x_1, x_2, x_3)$ et $\overrightarrow{W} = (w_1, w_2, w_3)$.
$\overrightarrow{X}$ est notre variable input_layer et
$\overrightarrow{W}$ la variable synaptic_weights.
Ensuite on applique la fonction sigmoid $\phi$ et on retrouve notre formule :
$$\widehat{y} = \phi \left( \sum_{i=1}^3 x_i w_i\right)$$
Lorsqu’on exécute le code à cette étape, voici ce qu’on obtient :
Poids synaptiques aléatoires:
[[-0.16595599]
[ 0.44064899]
[-0.99977125]]
Sorties après l'entraînement
[[0.2689864 ]
[0.3262757 ]
[0.23762817]
[0.36375058]]
Les trois premiers nombres sont les poids tirés au sort. Vous obtiendrez les mêmes car le générateur est initialisé avec une racine.
Les quatre nombres suivants sont les sorties prédites pour nos entrées.
Déception ! On est loin du compte.
Nos sorties sont très éloignées des nombres attendus (dernière colonne) :
| Input 1 | Input 2 | Input 3 | Outputs | |
|---|---|---|---|---|
| Exemple 1 | 0 | 0 | 1 | 0 |
| Exemple 2 | 1 | 1 | 1 | 1 |
| Exemple 3 | 1 | 0 | 1 | 1 |
| Exemple 4 | 0 | 1 | 1 | 0 |
Nous allons maintenant aborder l’entraînement qui nous permet d’améliorer ces résultats étape après étape afin de s’approcher des valeurs souhaitées.
L’entraînement #
Commençons par détailler les calculs effectués.
On prend notre premier exemple :
| Input 1 | Input 2 | Input 3 | Outputs | |
|---|---|---|---|---|
| Exemple 1 | 0 | 0 | 1 | 0 |
et nos poids aléatoires :
Poids synaptiques aléatoires:
[[-0.16595599]
[ 0.44064899]
[-0.99977125]]
On a donc :
$x_1 = 0,$
$x_2 = 0,$
$x_3 = 1$
et :
$w_1=-0.165,$
$w_2 = 0.440,$
$w_3=-0.999$
La somme pondérée :
$$\sum_{i=1}^3 x_i w_i = x_1w_1 + x_2w_2 + x_3w_3$$
$$\sum_{i=1}^3 x_i w_i = 0\times-0.165 + 0\times 0.440 + 1\times -0.999 = -0.999$$
On applique la fonction sigmoid $\phi$ à ce résultat :
$\phi(x) = \dfrac{1}{1+e^{-x}}$ donc $\phi(-0.999) = 0.2689\ldots$
Exactement ce qu’on a obtenu plus tôt :
Sorties après l'entrainement
[[0.2689864 ]
Le principe de l’entraînement #
- D’abord, on prend les les entrées d’entraînement et on les passe à la formule pour obtenir la sortie du neurone.
- On calcule l’erreur : la différence entre la sortie voulue et celle qu’on a obtenu.
- On ajuste les poids selon l’erreur obtenue.
- On répète 20.000 fois !
Ce principe s’appelle back propagation
Mais comment connaître l’ajustement à apporter aux poids ?
Dérivée pondérée par l’erreur : #
On multiplie l’erreur par l’entrée et par la dérivée de la fonction sigmoid.
ajustement des poids = erreur * input * derivee_sigmoid(sortie)
avec
erreur = sortie réelle - sortie obtenue
input = 0 ou 1
D’abord on s’assure que l’ajustement est proportionnel à l’erreur. Si l’erreur est petite, il faut un ajustement petit et inversement. Si l’entrée est 0, le poids n’est pas ajusté. Enfin on multiplie par la dérivée de la fonction sigmoid.
Mais pourquoi multiplier par la dérivée de la fonction sigmoid ?
Examinons en détail :
- On a déjà appliqué la fonction sigmoid avant la sortie du neurone (c’est important de s’en souvenir pour la suite)
- Si la sortie est un “grand” nombre (positif ou négatif), le neurone est plutôt confiant en ses résultats.
- Sur la graphique suivant, on voit que la pente de la fonction sigmoid est faible pour des valeurs élevées. Elle est forte autour de 0.
- Si la sortie est un “grand” nombre, on ne veut pas modifier énormément la réponse. Multiplier par la pente de la fonction sigmoid nous assure que ce sera le cas.
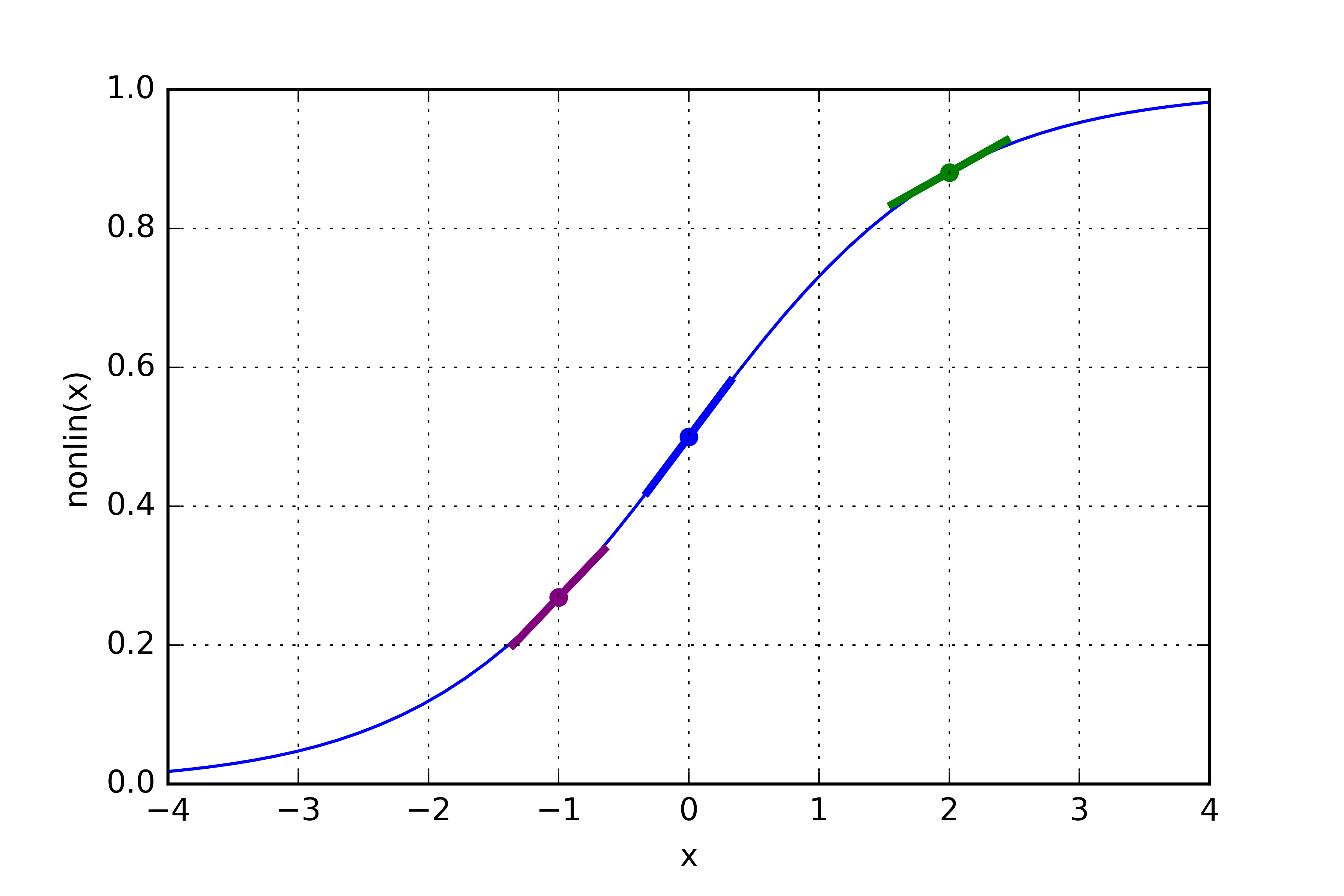
- Pour une valeur élevée (abscisse du point vert), la pente est faible.
- Pour des valeurs faibles (abscisse du point violet), la pente est forte.
- La pente est maximale en 0 (abscisse du point bleu).
La propogation #
Vers l’avant
- On donne les entrées,
- Et les poids,
- On envoie tout ça au neurone qui calcule…
- La sortie !
- On compare la sortie à la vraie valeur
Vers l’arrière
On ajuste les poids avec la formule vue plus haut :
ajustement des poids = erreur * input * derivee_sigmoid(sortie)
Et on recommence (20.000 fois).
Code de la deuxième partie #
On peut maintenant programmer ce procédé de backpropagation.
On commence par calculer l’erreur. Modifier la boucle comme ceci :
Seule la dernière ligne change.
# On itère 10000 fois
for iteration in range(10000):
# On défini la couche d'entrée
input_layer = training_inputs
# On normalise le produit des entrées par les poids synaptiques
outputs = sigmoid(np.dot(input_layer, synaptic_weights))
# Quelle est l'erreur commise ?
error = training_outputs - outputs
Ensuite on ajoute la dérivée de la fonction sigmoid.
Ici une remarque importante… on a déjà appliqué la fonction sigmoid à la somme pondérée. En quoi est-ce important ? Et bien la fonction sigma vérifie la relation suivante :
$$\phi’(x) = \phi(x)(1-\phi(x))$$
C’est un simple exercice de calcul de dérivée que vous pouvez vérifier sans difficulté.
En quoi est-ce intéressant ?
Si on connaît déjà la valeur de $\phi(x)$, il suffit de calculer $\phi(x)(1-\phi(x))$ pour obtenir la dérivée qui nous intéresse.
On ajoute donc, juste après la définition de sigmoid une fonction qui
permet de passer d’une image de $\phi$ à une image de $\phi’$.
def sigmoid_derivative(x):
'''
Calcule la dérivée de sigmoid
@param x: (float) l'entrée est déjà une image par sigmoid
@return: (float) la dérivée
'''
return x * (1 - x)
Il ne reste plus qu’à modifier la boucle pour intégrer les ajustements :
# On itère 10000 fois
for iteration in range(10000):
# On défini la couche d'entrée
input_layer = training_inputs
# On normalise le produit des entrées par les poids synaptiques
outputs = sigmoid(np.dot(input_layer, synaptic_weights))
# Quelle est l'erreur commise ?
error = training_outputs - outputs
# On multiplie notre erreur par la pente de la fonction sigmoid
# prise aux valeurs de sortie
# remarquons ici qu'on a déjà calculé la fonction simoid sur la sortie
# on obtient bien l'image de la dérivée de la fonction sigmoid
adjustments = error * sigmoid_derivative(outputs)
# on met les poids à jour
synaptic_weights += np.dot(input_layer.T, adjustments)
print("Poids synpatiques après l'entrainement : ")
print(synaptic_weights)
Plusieurs modifications :
- le nombre d’itérations
range(10000): testez d’abord avec 1 si vous n’êtes pas confiant adjustments: l’erreur (un nombre) multiplié par le vecteur des sorties auquel on a appliqué la fonctionsigmoid_derivativesynaptic_weightsqu’on modifie par un produit scalaire, celui du vecteur des entrées par le vecteur des ajustements.- On n’affiche les poids finaux qu’après la boucle, pas à chaque tour.
Quand on exécute ce code on obtient les résultats suivants :
Poids synaptiques aléatoires:
[[-0.16595599]
[ 0.44064899]
[-0.99977125]]
Poids synpatiques après l'entrainement :
[[ 9.67299303]
[-0.2078435 ]
 [-4.62963669]]
Sorties après l'entrainement
[[0.00966449]
[0.99211957]
[0.99358898]
[0.00786506]]
Ce qui correspond bien aux résultats espérés :
| Input 1 | Input 2 | Input 3 | Outputs | |
|---|---|---|---|---|
| Exemple 1 | 0 | 0 | 1 | 0 |
| Exemple 2 | 1 | 1 | 1 | 1 |
| Exemple 3 | 1 | 0 | 1 | 1 |
| Exemple 4 | 0 | 1 | 1 | 0 |
La fonction sigmoid ne renverra jamais $0$ ou $1$ mais seulement des nombres très proches. Voilà pourquoi on obtient $0.00966449 \approx 0$ ou $0.99211957 \approx 1$.
Une fois que ça fonctionne, vous pouvez essayer avec $100.000$ itérations, ce sera légèrement plus long mais vos résultats vont s’approcher de $0$ et de $1$.
Il faudrait un nombre infini d’étapes pour obtenir exactement $0$ ou $1$.
Conclusion #
Voilà la fin de cette première partie dans laquelle on a crée un simple réseau de neurone (1 seul neurone !) qui utilise la backpropagation pour améliorer ses prédictions.
Il est capable de s’entraîner correctement… mais on ne l’a pas encore testé sur de nouvelles valeurs !
Dans la seconde partie nous allons englober ce neurone dans une classe afin de tester sa qualité.