5. second TD #

1. Éclairage #

Il y a une longue allée dans le jardin d’Alice avec n marches d’escalier placées de manière irrégulière aux positions $x_i$ pour $i \in 1\ldots n$. Elle souhaite donc installer des lanternes sur le chemin pour éviter que ses invités ne choient s’ils s’aventurent au clair de lune. Elle a repéré un modèle de lanternes de portée $p$ qui lui plaît bien mais qui est un peu cher.

Proposer un algorithme glouton pour aider Alice à placer un nombre minimum de lanternes permettant d’éclairer chaque marche.
Votre algorithme est-il optimal ? Justifiez.
En combien d’étapes au maximum s’arrête votre algorithme ? Il ne reste que k lanternes en stock lorsqu’Alice fait ses courses.
Alice aura-t-elle assez de lanternes pour éclairer tout le chemin ?

Supposons maintenant qu’une de ses amies, médium, soit capable, sans calculer le nombre minimum de lanternes, de décider si un nombre $k$ de lanternes est suﬃsant lorsqu’on lui donne la liste des positions des marches. Alice peut la consulter autant de fois qu’elle le souhaite. 5. Proposer un algorithme le plus eﬃcace possible pour aider Alice à trouver le nombre minimum de lanternes permettant d’éclairer chaque marche.

Alice a enfin fixé sa liste d’invités et pense maintenant au menu. Malheureusement ses invités sont très difficiles, mais elle connaît l’ensemble $s i$ de plats parmi les $n$ qu’elle sait préparer et qui conviennent à l’invité $i$ pour $i \in 1\ldots m$. Consciente qu’elle n’aura peut être pas le temps de préparer les $n$ plats, Alice aimerait trouver un ensemble de plats qui assure que chaque invité trouvera son bonheur sur le buffet.

Proposer un algorithme glouton pour aider Alice à faire son menu.
Votre algorithme est-il optimal ? Justifiez
En combien d’étapes au maximum s’arrête votre algorithme ?

3. Déménagement #

Alice doit déménager et pour cela ranger toutes ses affaires dans des cartons. Pour faire le moins de trajets possibles dans l’escalier elle souhaite réussir à utiliser le moins de cartons possible. Cependant elle estime ne pas pouvoir porter des cartons de plus de $C$ grammes. Alice connaît le poids $p_i$ de chacun des $n$ objets à placer dans les cartons, pour $i \in 1\ldots n$ et dispose d’autant de cartons identiques qu’elle le souhaite.

Proposer un algorithme glouton pour aider Alice à faire ses cartons.
Votre algorithme est-il optimal ? Justifiez
En combien d’étapes au maximum s’arrête votre algorithme ?

4. Ranger les malles du Père Noël #

Le Père Noël est en plein préparatif de la grande nuit. Le doit ranger dans les malles de son traîneau les cadeaux destinés aux enfants. Il veut optimiser son rangement de façon à utiliser le moins de malles possibles.

Pour simplifier, chaque cadeau est modélisé par son nom et sa taille.

Chaque malle est modélisée par une liste de cadeaux, et le traîneau sera modélisé par une liste de malles.

Exemple

train = {"nom": "train",   "taille": 18}
nours = {"nom": "peluche", "taille": 48}
stylo = {"nom": "stylo",   "taille": 1}
velo  = {"nom": "velo",    "taille": 25}
liste_cadeaux = [train, nours, stylo, velo]
malle1 = [train, stylo]
malle2 = [velo, {"nom": "console", "taille": 5}]
malle3 = [nours]
traineau = [malle1, malle2, malle3]

a. Combien de cadeaux y a-t-il dans liste_cadeaux ?

b. Combien de cadeaux y a-t-il dans malle2 ?

c Combien de malles y a-t-il dans traineau ?

On ajoute la contrainte suivante : chaque malle a une contenance maximale, les cadeaux qu’elle contient ne peuvent totaliser une taille supérieure à 50.

a. Montrer que la place occupée par les cadeaux dans malle2 est égale à 30.

b. Quelle est la contenance disponible de malle1 ?

c. Écrire le code de la fonction place_occupee qui prend en paramètre une malle et qui renvoie la place occupée par les cadeaux de cette malle. Écrire au moins un test. On ne demande pas la documentation dans cette question.

d. Écrire le code de la fonction place_disponible qui prend en paramètre une malle et qui renvoie la contenance disponible dans cette malle. Écrire au moins un test. On ne demande pas la documentation dans cette
```
question.
```
Pour minimiser le nombre de malles nécessaires, les lutins du Père Noël décident d’utiliser l’algorithmes glouton suivant :

Données :
- une liste de cadeaux.
Résultat : un traîneau, c’est-à-dire une liste de malles.

Algorithme :
1. Initialiser traineau à une liste vide.
2. Initialiser nouvelle_malle à une liste vide.
3. Ajouteur nouvelle_malle au traineau.
4. Pour chaque cadeau de la liste : Si la taille du cadeau est inférieure à la contenance disponible de nouvelle_malle ajouter le cadeau à nouvelle_malle.
  
  Sinon :
  - créer une nouvelle_malle dans laquelle on mettra le cadeau ;
  - ajouter cette nouvelle_malle au traîneau.
5. Renvoyer traineau
Que renvoie cet algorithme avec la liste_cadeaux donnée à la question 1. ?

Montrer que, pour cet exemple, l’algorithme ne donne pas la solution optimale.
Proposez une implémentation en Python de l’algorithme des lutins. Écrire au moins un test. On ne demande pas la documentation dans cette question.

Compléments de Gilles Lassus #

Notebook sur Github

Remplir un rectangle avec des carrés #

(d’après S.Tummarello et E.Buonocore)

On considère un rectangle de dimension 11 sur 13 (figure 0). On veut remplir ce rectangle avec le minimum de carrés.

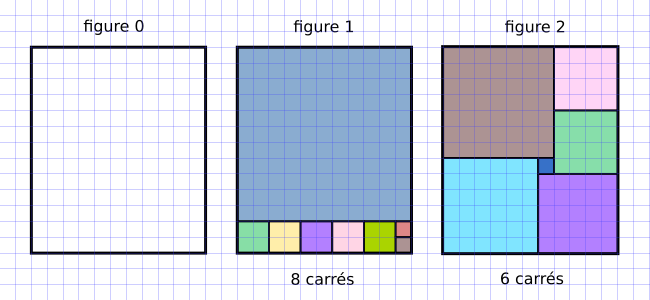
Exemple 1

Un algorithme glouton va chercher à positionner d’abord le plus grand carré possible (figure 1).

C’est une stratégie efficace (8 carrés nécessaires), mais qui n’est pas optimale : la figure 2 présente un pavage avec seulement 6 carrés.

Est-ce qu’un algorithme glouton va toujours passer à côté de la solution optimale ? Non ! Il arrive aussi qu’il donne la solution optimale. Changeons le rectangle initial en un rectangle de 10 sur 15 :

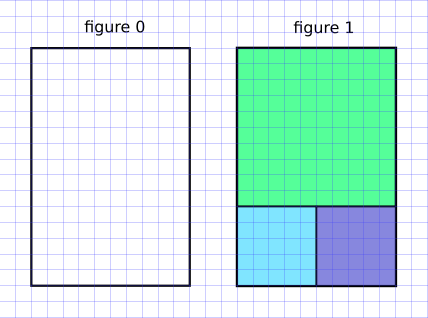
Exemple 2

Dans cette situation, l’algorithme glouton nous amène à la solution optimale.

Conclusion : #

Un algorithme glouton est une méthode rapide et souvent efficace, mais qui ne garantit pas l’optimalité de la solution trouvée.

La succession de meilleurs choix LOCAUX va nous amener à une bonne solution GLOBALE, mais ne nous garantit pas d’arriver à la solution optimale.

Consigne #

Proposer un algorithme glouton permettant de remplir un rectangle.

L’objectif est de créer une fonction remplir_glouton qui prend deux paramètres entiers largeur et hauteur et renvoie une liste de tuples : [(abs_1, ord_1, largeur_1), (abs_2, ord_2, largeur_2), ...] donnant les positions de chaque rectangle.

5. TD