pdf: pour impression

Qu’est-ce qu’un arbre ? #

Dessinons un arbre !

Arbre en informatique #

Les arbres sont des structures de données¹

hiérarchiques,
naturellement récursives,

utilisées pour représenter des ensembles de données structurées hiérarchiquement.

Quelques exemples #

En biologie :

.
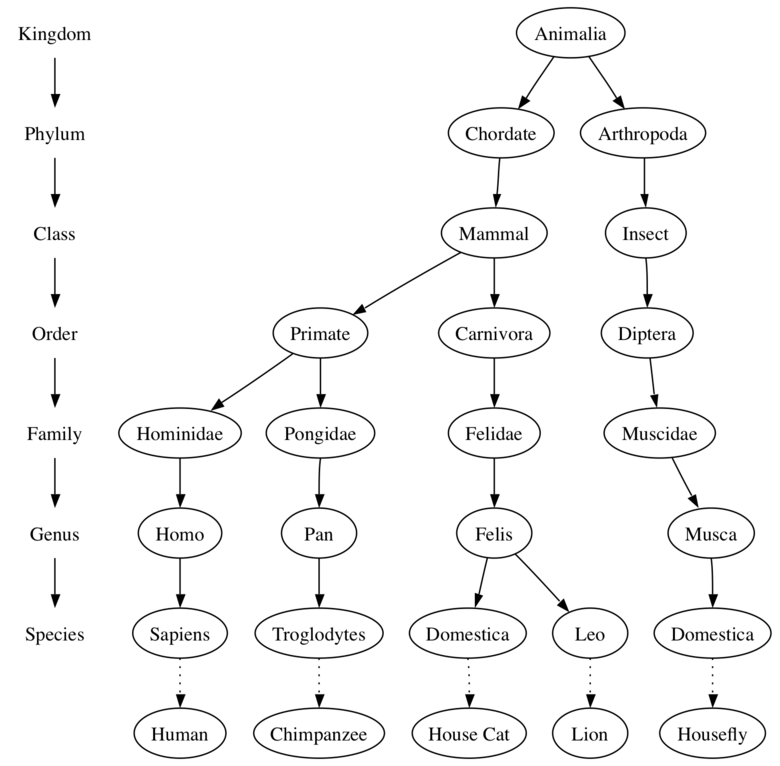
Les dossiers d’un ordinateur

.

Les balises d’une page web forment un arbre (appelé DOM) :

<html xmlns="http://www.w3.org/1999/xhtml"
      xml:lang="en" lang="en">
<head>
    <meta http-equiv="Content-Type"
          content="text/html; charset=utf-8" />
    <title>simple</title>
</head>
<body>
<h1>A simple web page</h1>
<ul>
    <li>List item one</li>
    <li>List item two</li>
</ul>
<h2><a href="http://www.cs.luther.edu">Luther CS </a><h2>
</body>
</html>

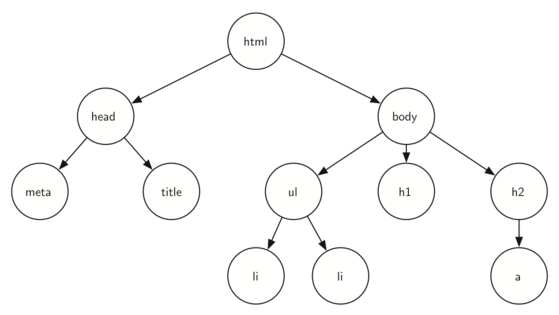
. structure d’une page web

Un arbre est une structure de données non-linéaire (comparée aux tableaux, listes, piles, et files qui sont des structures linéaires).

Une structure de données arborescente peut être définie récursivement comme un ensemble de nœuds accessibles depuis un nœud racine. Chaque nœud étant une structure composée d’une valeur et d’une liste de références vers d’autres nœuds, avec les contraintes suivantes : aucune référence n’est dupliquée (chaque nœud a un unique parent), et aucune référence ne désigne le nœud racine (qui n’a donc pas de parent).

Nous allons nous restreindre aux arbres binaires pour lesquels la liste des références vers d’autres nœuds comporte au plus deux éléments.
Ces arbres binaires sont largement utilisés, par exemple sous forme d’ABR – arbres binaires de recherche –, de tas, d’arbres équilibrés comme les AVL, ou encore d’arbres bicolores rouge-noir.

Un peu (beaucoup…) de vocabulaire préliminaire #

→ Terminologie #

un nœud est caractérisé par
- une donnée (on parle aussi d’étiquette),
- un nombre fini de fils.
une arête relie deux nœuds. Chaque nœud, à l’exception de la racine, est relié à un autre nœud, son père, par exactement une arête entrante. Chaque nœud peut avoir une ou plusieurs arêtes sortantes le reliant à ses fils. On parle aussi de lien.
la racine d’un arbre est le seul nœud sans père.
un chemin est une liste de nœuds reliés par des arêtes.
une branche est le chemin le plus court reliant un nœud à la racine.
les fils sont l’ensemble des nœuds reliés à un même nœud par des arêtes entrantes.
le père ou parent est le nœud relié à ses nœuds fils par une arête sortante.
un sous-arbre est l’ensemble des nœuds et arêtes d’un nœud parent et de ses descendants.
une feuille est un nœud sans fils.
un nœud interne est un nœud qui n’est pas une feuille.

Pour assurer la cohérence de ces définitions, on considère que l’arbre vide n’est pas un nœud.

→ Quelques mesures sur les arbres #

la taille d’un arbre est le nombre de nœuds de l’arbre.
la profondeur d’un nœud est le nombre d’arêtes sur la branche qui le relie à la racine. La profondeur de la racine est nulle.
la hauteur d’un arbre est la profondeur maximale de l’ensemble des nœuds de l’arbre.

Attention dans la définition précédente, la hauteur de l’arbre vide est -1. Celle d’un arbre ne contenant qu’une racine est 0.

Il existe une autre définition dans laquelle la hauteur d’un arbre vide est 0 et celle d’un arbre ne contenant qu’une racine est 1.

Aucun consensus clair n’est établi à ce propos en informatique et les usages varient… y compris dans les sujets de bac.

Vous prendrez donc garde à la définition employée dans un énoncé.
l’arité d’un nœud est le nombre de fils du nœud.
l’arité d’un arbre est le nombre maximal de fils des nœuds de l’arbre.

→ Définition. Arbre binaire #

Un arbre binaire est donc un arbre d’arité deux.

Un arbre binaire est

soit l’arbre vide, noté $\Delta$ ;
soit un triplet (e, g, d), appelée nœud, dans lequel
- e est l’élément, ou encore étiquette, de la racine de l’arbre,
- g est le sous-arbre gauche de l’arbre, et
- d est le sous-arbre droit de l’arbre.

Les sous-arbres gauche et droit d’un arbre binaire non vide sont eux-mêmes des arbres binaires. La structure d’arbre binaire est donc une structure récursive.

on appelle fils gauche, resp. fils droit, le sous-arbre gauche, resp. droit, d’un nœud.

Se familiariser avec les arbres binaires #

$\gg$ Quelques arbres binaires #

Dessinez chacun des arbres ci-dessous, donnez sa taille et sa hauteur, le nombre de feuilles, le nombre de nœuds à chaque profondeur.

(1, $\Delta$, $\Delta$)
(3, (1, $\Delta$, (4, (1, $\Delta$, (5, $\Delta$, $\Delta$)), $\Delta$)), $\Delta$)
(3, (1, (1, $\Delta$, $\Delta$), $\Delta$), (4, (5, $\Delta$, $\Delta$), (9, $\Delta$, $\Delta$)))
(3, (1, (1, $\Delta$, $\Delta$), (5, $\Delta$, $\Delta$)), (4, (9, $\Delta$, $\Delta$), (2, $\Delta$, $\Delta$)))

$\gg$ Des arbres binaires #

Combien de feuilles au minimum comporte un arbre binaire de hauteur h ?
Au maximum ?
Combien de nœuds au minimum comporte un arbre binaire de hauteur h ?
Au maximum ?

$\gg$ Squelettes d’arbres binaires #

On appelle squelette ou forme d’arbres binaires tout arbre binaire dans lequel on ne tient pas compte des étiquettes.

Combien y a-t-il de squelettes d’arbres binaires de taille 0, de taille 1 ?

Dessinez tous les squelettes d’arbres binaires de taille 2, 3, 4 ; donnez-en le nombre.

$\gg$ Taille et hauteur #

Proposez des algorithmes pour calculer

la taille d’un arbre binaire
la hauteur d’un arbre binaire. On conviendra conventionnellement que la hauteur de l’arbre vide $\Delta$ est -1.

Remarque importante

On rencontre plusieurs définitions de la hauteur… jusque dans les énoncés de bac. L’informatique est toujours une science récente et certaines définitions ne sont pas arrêtées.

Si la hauteur de la racine est 0

hauteur #

Si la hauteur de la racine est 0, cet arbre a pour hauteur 2.
Si la hauteur de la racine est -1, cet arbre a pour hauteur 1.

Il faudra vous adapter au contexte, qui le précise toujours.

Caractériser les arbres binaires #

Les arbres binaires sont caractérisés par le fait que chaque nœud possède au plus deux fils.

D’autres caractéristiques sont définies, qui permettent par exemple d’identifier des arbres pour lesquels le coût de certaines opérations sera minimal, ou de définir des algorithmes spécifiques à ces arbres.

Un arbre binaire filiforme ou dégénéré est un arbre dans lequel tous les nœuds internes n’ont qu’un seul fils.
(Un arbre filiforme ne possède donc qu’une unique feuille.)
Un arbre binaire localement complet ou arbre binaire strict est un arbre dont tous les nœuds internes possèdent exactement deux fils.
(Autrement dit, un arbre binaire localement complet est un arbre dont chaque nœud possède zéro ou 2 fils. L’arbre vide n’est pas localement complet.)
Un arbre binaire complet est un arbre binaire localement complet dans lequel toutes les feuilles sont à la même profondeur.
(Il s’agit d’un arbre dont tous les niveaux sont remplis.)
Un arbre binaire parfait est un arbre dans lequel tous les niveaux sont remplis à l’exception éventuelle du dernier, et dans ce cas les feuilles du dernier niveau sont alignées à gauche.
Un arbre binaire équilibré est un arbre dont les deux fils sont des arbres équilibrés dont les hauteurs diffèrent d’au plus une unité.
Ainsi, l’accès à n’importe lequel des nœuds est en moyenne minimisé.

_Comme le mentionne la page Wikipedia _Arbre_binaire#Types_d’arbres_binaires_, il existe des usages contradictoires des termes complet et parfait qui peuvent parfois être intervertis. Des confusions peuvent aussi exister entre le français et l’anglais, dans lequel on trouve les termes perfect et complete.
La terminologie utilisée ici est cohérente avec celle de Froidevaux et al.², alors que Beauquier et al.³ en utilisent une autre._

Se repérer dans cette forêt d’arbres #

$\gg$ Compter ces arbres #

Combien de nœuds au maximum comporte un arbre localement complet de hauteur h ?
Au minimum ?
Combien de nœuds comporte un arbre complet de hauteur h ?
Combien de squelettes d’arbres parfaits de hauteur h existe-t-il ?
Combien de squelettes d’arbres filiformes de hauteur h exite-t-il ?

$\gg$ Reconnaître ces arbres #

Proposez des algorithmes pour les prédicats

reconnaître un arbre binaire filiforme
reconnaître un arbre binaire localement complet
reconnaître un arbre binaire complet
reconnaître un arbre binaire parfait

$\gg$ Superposer deux arbres #

Proposez un prédicat pour tester l’égalité du squelette de deux arbres binaires.

$\gg$ Numéroter les nœuds #

La numérotation de Sosa-Stradonitz des nœuds d’un arbre binaire, utilisée notamment en généalogie, est la suivante :

le nœud racine est numéroté par 1
si un nœud numéroté par $i$
- son fils gauche est numéroté par $2i$
- son fils droit est numéroté par $2i + 1$

Cette numérotation peut être utilisée pour représenter un arbre dans un tableau : l’élément $j$ du tableau mémorise le nœud numéroté par $j$.

Combien d’éléments doit contenir un tableau utilisé pour représenter

un arbre binaire complet de $n$ nœuds ?
un arbre binaire parfait de $n$ nœuds ?
un arbre binaire quelconque de $n$ nœuds (dans le pire des cas) ?

À suivre… #

Il s’agira de

parcourir les arbres
identifier les opérations primitives pour manipuler les arbres

et de découvrir les ABR, arbres binaires de recherche.

Le terme d’arbre recouvre plusieurs notions distinctes : arbres libres, arbres enracinés, arbres binaires, etc.
Nous ne traiterons pas des arbres libres qui relèvent de la théorie des graphes.
Nous nous intéresserons aux arbres enracinés que nous nommerons plus simplement arbres, et aux arbres binaires, un cas particulier de ces arbres enracinés. ↩︎
Types de données et algorithmes, Christine Froidevaux, Marie-Claude Gaudel, Michèle Soria. McGraw-Hill (Paris, 1990), Ediscience (1994). Téléchargeable depuis la page de Marie-Claude Gaudel lri.fr/~mcg/
↩︎
Eléments d’algorithmique Danièle Beauquier, Jean Berstel, Philippe Chrétienne. Masson (1992 pour la 1re édition). Téléchargeable depuis la page de Jean Berstel www-igm.univ-mlv.fr/~berstel/
↩︎

Arbres - TD 1