pdf : pour impression, diapo avec anim, diapo sans anim

Récursivité #

Définition #

Larousse :
- récursivité :
Propriété que possède une règle ou un élément constituant de pouvoir se répéter de manière théoriquement indéfinie. (C’est une propriété essentielle des règles d’une grammaire générative, celle qui permet d’engendrer un nombre infini de phrases.)

Qualité d’un programme informatique récursif.

Théorie destinée à fournir un cadre rigoureux à l’étude des notions intuitives de calculabilité et de décidabilité effectives. (Church a montré [1936] que la récursivité est l’équivalent mathématique de la calculabilité effective : la fonction récursive est une fonction rigoureusement calculable.)
- récursif :
Se dit d’une règle ou d’un élément doués de récursivité. Se dit d’un programme informatique organisé de manière telle qu’il puisse se rappeler lui-même, c’est-à-dire demander sa propre exécution au cours de son déroulement.

Avec au passage, un bel exemple de récursivité (croisée).
Wikipédia :
La récursivité est une démarche qui fait référence à l’objet même de la démarche à un moment du processus. En d’autres termes, c’est une démarche dont la description mène à la répétition d’une même règle. Ainsi, les cas suivants constituent des cas concrets de récursivité :
- décrire un processus dépendant de données en faisant appel à ce même processus sur d’autres données plus « simples » ;
- montrer une image contenant des images similaires ;
- définir un concept en invoquant le même concept ;
- écrire un algorithme qui s’invoque lui-même ;
- définir une structure à partir de l’une au moins de ses sous-structures.

Exemples #

processus récursif #

Calcul de la fonction dérivée d’une fonction dérivable

Entrée : f (une fonction dérivable) - Sortie : f’ (la fonction dérivée)

derivee(f) =
    si f est une fonction élémentaire de base
        renvoyer sa dérivée
    sinon si f == u+v
        renvoyer derivee(u) + derivee(v)
    sinon si f == u × v
        renvoyer derivee(u)×v + u×derivee(v)
    sinon si …

Production de fractales :

On dispose de la primitive tracer(l) qui permet de tracer un segment de longueur l.

Le processus de tracé d’un segment de von koch de taille l à l’ordre n est :

vonkoch(l,n)

si n = 1, tracer(l)
sinon
- vonkoch(l/3, n-1)
- tourner à gauche de 60°
- vonkoch(l/3, n-1)
- tourner à droite de 120°
- vonkoch(l/3, n-1)
- tourner à gauche de 60°
- vonkoch(l/3, n-1)

Le flocon est obtenu en traçant 3 segments de von koch séparés par des rotations à droite de 120°.

flocon

NB Se réalise très bien avec la tortue (module turtle), tracer(l) = forward(l) et les fonctions rightet left permettent les rotations

Images #

Print gallery M.C.Escher
La vache qui rit

)
Pochette Ummagumma de Pink Floyd

Sigles #

VISA : VISA International Service Association
GNU : GNU is Not Unix
WINE : Wine Is Not an Emulator
Bing : Bing is not Google (non officiel)
LAME : Lame Ain’t an MP3 Encoder

Grammaire #

Un groupe nominal est composé d’un nom ou d’un nom et son complément. Le complément d’un nom est soit un adjectif, soit un adverbe, soit un groupe nominal. (très approximativement)

groupe_nominal ::=    nom
                    | nom complement
complement     ::=    adjectif
                    | adverbe
                    | groupe_nominal

Algorithme récursif #

Le tri rapide : cf. reference sur site U. Lille :

Structures récursives #

Certaines structures de données sont naturellement récursives.

listes, arbres

Une liste est une structure de données.

Elle peut être vide.
Lorsqu’elle n’est pas vide, elle contient deux objets : un élément et un pointeur vers une autre liste.

plus de détails plus bas !

Algorithmes récursifs #

Définition #

Un algorithme de résolution d’un problème P sur une donnée a est dit récursif si parmi les opérations utilisées pour le résoudre, on trouve la résolution du même problème P sur une donnée b. Dans un algorithme récursif, on nomme appel récursif toute étape de l’algorithme résolvant le même problème sur une autre donnée.

Exemple #

Ne faisons pas dans l’originalité, la factorielle :

$$n! = n \times (n-1)! \text{ si } n > 1 \text{ et } 0! = 1$$

Principe :

  5! = 5 x 4!
     = 5 x 4 x 3!
     = 5 x 4 x 3 x 2!
     = 5 x 4 x 3 x 2 x 1!
     = 5 x 4 x 3 x 2 x 1 x 0!
     = 5 x 4 x 3 x 2 x 1 x 1
     = 120

Programmation #

def fact(n):
    if n <= 1:
        return 1
    else:
        return n * fact(n-1)

>>> fact(5)
120

Déroulement de l’exécution #

Mise en évidence :

avec le debugger de Thonny
avec PythonTutor

On observe la construction de la pile des appels successifs de la fonction. Chaque appel possède son propre environnement, donc ses propres variables.

La pile est nécessaire pour mémoriser les valeurs propre à chaque appel.

def fact(n):
    """Version légèrement différente avec un seul return"""
    if n <= 1:
        result = 1
    else:
        result = n * fact(n - 1)
    return result

fact(5)         # s'évalue à 120

Dans PythonTutor

Ordre des appels récursifs #

Déroulement des appels récusifs #

Lorsqu’on appelle une fonction récusive :

Python entre dans la fonction et crée un appel initial.
Il calcule tout ce qu’il peut jusqu’à rencontrer l’appel récursif…
Python entre dans la fonction et crée un appel
Il calcule tout ce qu’il peut jusqu’à rencontrer l’appel récursif…
Python entre dans la fonction et crée un appel
…
Lorsqu’on arrive au cas de base, Python renvoie la valeur à l’appel dont il est issu
L’appel reçoit la valeur, termine son calcul et renvoie la valeur à l’appel dont il est issu
L’appel reçoit la valeur, termine son calcul et renvoie la valeur à l’appel dont il est issu
…
L’appel initial reçoit la valeur, termine son calcul et renvoie la valeur à l’appel initial.

Seules les premières et dernières étapes sont visibles.

Taille de la pile des appels récusifs #

Attention En Python la taille de la pile des appels récursifs est limitée. Si la récursivité est trop profonde et que l’on atteint cette limite, on déclenche une RecursionError.

La valeur de cette pile peut être obtenue par :

>>> import sys
>>> sys.getrecursionlimit()
3000

et modifiée par

>>> sys.setrecursionlimit(100)
>>> fact(100)
  Traceback (most recent call last):
  File "<pyshell>", line 1, in <module>
  File "C:\Users\JC\Documents\jc\enseignement\diu\bloc1\supports\recursivite\src\recursivite.py", line 16, in fact
    return n * fact(n-1)
  ...
  File "C:\Users\JC\Documents\jc\enseignement\diu\bloc1\supports\recursivite\src\recursivite.py", line 13, in fact
    if n <= 1:
  RecursionError: maximum recursion depth exceeded in comparison

Eléments Caractéristiques #

Un programme récursif est constitué de deux parties :
Le cas de base.
il faut au moins une situation qui ne consiste pas en un appel récursif.
   if n <= 1:
      return 1
Cette situation est appelée situation de terminaison ou situation d’arrêt ou cas d’arrêt ou cas de base.
Un appel récursif.
chaque appel récursif doit se faire avec des données qui permettent de se rapprocher d’une situation de terminaison
        return n * fact(n-1)
Il faut s’assurer que la situation de terminaison est atteinte après un nombre fini d’appels récursifs.

La preuve de terminaison d’un algorithme récursif se fait en identifiant la construction d’une suite strictement décroissante d’entiers positifs ou nuls.

Remarque: Dans le cas de factorielle, il s’agit simplement de la suite des valeurs du paramètre.

Mauvaise conception récursive #

Respecter la première règle ne suffit pas :

def fact(n):
    if n <= 1:
        return 1
    else:
        return fact(n+1)/(n+1)

Ce programme ne termine pas

Un autre exemple #

Il faut trouver un énoncé récursif de résolution du problème, c’est-à-dire un énoncé qui fasse référence au problème lui-même.

Exemple : calculer le nombre d’occurrences d’un caractère dans une chaîne.

Énonce :

Cas de base

Le nombre d’occurrences de c dans s est 0 si s est vide.
Appel récursif
- Si c est le premier caractère de s, on ajoute 1 au nombre d’occurrences de c dans les autres caractères de s.
- Sinon, il s’agit du nombre d’occurrences de c dans les autres caractères de s.

def occurrences(char, string):
    if string == "":
        return 0
    elif char == s[0]:
        return 1 + occurrences(char, string[1:])
    else:
        return occurrences(char, string[1:])

La terminaison se vérifie en considérant la suite des longueurs des chaînes passées en paramètre.

Récursivité terminale (tail recursion) #

Un algorithme récursif simple est terminal lorsque l’appel récursif est le dernier calcul effectué pour obtenir le résultat. Il n’y a pas de “calcul en attente”. L’avantage est qu’il n’y a rien à mémoriser dans la pile.

Remarques:

Ce n’est pas le cas des deux exemples précédents fact et occurrences.
Certains langages tirent partie de la récursion terminale pour accélérer un programme : C, Scheme…
Certains langages le font parfois : Rust, JavaScript…
D’autres ne le font pas du tout : Python

Hormis pour la lisibilité du code (et c’est important), il n’y a aucune amélioration de l’exécution d’un programme Python lorsqu’on écrit un programme récursif avec une récursivité terminale.

Exemple d’algorithme récursif terminal

Prédicat de présence d’un caractère dans une chaîne :

Un caractère c est présent dans une chaîne s non vide, s’il est le premier caractère de s ou s’il est présent dans les autres caractères de s. Il n’est pas présent dans la chaîne vide.

def est_present(char, string):
    if string == '':
        return False
    elif char == s[0]:
        return True
    else:
        return est_present(char, string[1:])

Voir le comportement avec PythonTutor, le debugger de Thonny ou le décorateur @trace.

Rendre terminal un algorithme récursif

On utilise un accumulateur, passé en paramètre, pour calculer le résultat au fur et à mesure des appels récursifs.

La valeur de retour du cas de base devient la valeur initiale de l’accumulateur et lors d’un appel récursif, le “calcul en attente” sert à calculer la valeur suivante de l’accumulateur.

Ainsi on obtient :

def fact_term(n, acc = 1):
    if n <= 1:
        return acc
    else:
        return fact_term(n-1, acc * n)

def occurrences_term(c,s, acc = 0):
    if s == "":
       return acc
    elif c == s[0]:
         return occurrences_term(c,s[1:], acc + 1)
    else:
         return occurrences_term(c,s[1:], acc)

Récursivité croisée #

La définition précédente des algorithmes récursifs ne couvre pas les cas des algorithmes mutuellement récursifs.

Exemple typique (et très classique) :

def pair(n):
    if n == 0:
       return True
    else:
       return impair(n-1)

def impair(n):
    if n == 0:
       return False
    else:
       return pair(n-1)

Récursivité multiple #

Un algorithme récursif est multiple si l’un des cas qu’il distingue se résout avec plusieurs appels récursifs.

C’était le cas de l’algorithme de dérivation.

Autre exemple avec le tri rapide

Retour sur les coefficients binomiaux

(ou un exemple où la récursivité, bien que naturelle, n’est pas adaptée)

Pour calculer les coefficients binomiaux on peut utiliser une formule directe : $\binom{n}{p} = \dfrac{n!}{p!(n-p)!}$

Mais vous connaissez aussi la relation de récurrence :

$\binom{n}{p} = 1$ si $n=p$ ou $n=0$
$\binom{n}{p} = \binom{n-1}{p} + \binom{n - 1}{ p - 1}$ si $n > p > 0$

Ce qui donnerait en Python

def C(n,p):
    if p == 0:
        return 1
    elif n == p:
        return 1
    else:
        return C(n-1, p-1) + C(n-1, p)

On peut observer l’explosion combinatoire du nombre d’appels récursifs et les redondances des calculs.

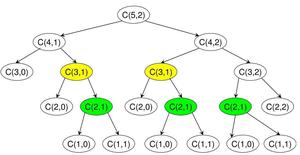
binomial

Certains coefficients binomiaux sont calculés plusieurs fois, sans réutiliser les résultats précédents.

Dans un tel cas, si on veut utiliser efficacement la récursivité, il faudraitt la coupler à un mécanisme de memoïsation (Wikipedia) qui permet d’éviter de refaire plusieurs fois le même calcul.

C’est ce que nous ferons plus tard en programmation dynamique.

Structures récursives #

Les listes Python sont des listes à “base de tableau”. D’ailleurs le programme de NSI parle explicitement de tableaux et mentionne “Python identifie listes et tableaux”. En fait les listes de Python sont des tableaux dynamiques, c’est-à-dire des tableaux dont la taille peut varier. Il n’en est pas de même dans tous les langages (exemple Java) (NB : en javascript, le type Array se comporte comme les listes Python).

De manière plus formelle, les listes sont des structures de données dynamiques et intrinsèquement récursives. Elles se définissent ainsi :

Une liste d’éléments de type T est

soit la liste vide
soit un couple (t,R) où t est de type T et R est une liste d’éléments de type T

Dans le cas d’une liste non vide (t,R) :

t est le premier élément de la liste aussi appelée tête de la liste
R est la liste des éléments qui suivent t, également appelée reste de la liste

On parle pour de telles structures de listes chaînées, qui se distingue donc des listes par tableaux.

liste

Les listes chainées sont beaucoup plus efficaces que les tableaux lorsqu’il s’agit de supprimer un élément, ou d’en insérer un.

Avec cette définition des listes, la définition d’une constante pour la liste vide ([]) et de primitives permettant

de construire un couple (x, R) ([x]+R)
d’accéder à la tête d’une liste non vide (l[0])
d’accéder au reste d’une liste non vide (l[1:])

suffit pour définir tous les traitements sur les listes. L’écriture de ces traitements se fait alors à l’aide de fonctions récursives.

Longueur d’une liste :

def length(liste):
    if liste == [] :
        return 0
    else:
        return 1 + length(liste[1:])

Nombre d’occurrences dans une liste :

def nb_occurrences(valeur, liste):
    if liste == [] :                        # quid de length(liste) == 0 ?
        return 0
    elif valeur == liste[0]:
        return 1 + nb_occurrences(valeur, liste[1:])
    else:
        return nb_occurrences(valeur, liste[1:])

NB Le langage Lisp se basait sur cette structure de données (Lisp = List Processing).

Quelques erreurs “classiques” #

attention aux effets de bord #

(peut ne pas être une erreur, mais il faut être vigilant…)

def length_destroy(liste):
    '''
    >>> length_destroy([]) == 0
    True
    >>> length_destroy([1,2,3]) == 3
    True
    '''
    if liste == [] :
        return 0
    else:
        liste.pop()  # pop() retire dernier élément de liste
        return 1 + length_destroy(liste)

Observons le comportement dans PythonTutor

oubli du return #

Pour certains étudiants, le return n’est pas nécessaire dans le cas récursif. Pour eux, le return du cas de base suffit, puisque l’on renvoie un résultat. Ils écrivent donc :

def fact(n):
    if n <= 1:
        return 1
    else:
        n * fact(n-1)

C’est encore plus vrai (pour eux) dans le cas d’un algorithme récursif terminal puisque, selon eux, le résultat est obtenu au cas d’arrêt…

def est_present(c,s):
    if s == '':
        return False
    elif c == s[0]:
        return True
    else:
        est_present(c,s[1:])

absence de prise de conscience de la localité des environnements #

Il s’agit d’une confusion entre une écriture itérative, basée sur des affectations de variables, et l’écriture récursive qui s’appuie sur la modification des paramètres.

Pour ces étudiants, les calculs sont faits (cf. l’incrémentation ci-dessous) et les appels récursifs aussi…

def occurrences_erreur(c,s):
    result = 0
    if s == "":
        result = 0
    elif c == s[0]:
        result = result + 1
        occurrences_erreur(c,s[1:])
    else:
        occurrences_erreur(c,s[1:])
    return result

Observons dans PythonTutor

Cours

Récursivité #

Définition #

Exemples #

processus récursif #

Images #

Sigles #

Grammaire #

Algorithme récursif #

Structures récursives #

Algorithmes récursifs #

Définition #

Exemple #

Programmation #

Déroulement de l’exécution #

Ordre des appels récursifs #

Déroulement des appels récusifs #

Taille de la pile des appels récusifs #

Eléments Caractéristiques #

Mauvaise conception récursive #

Un autre exemple #

Récursivité terminale (tail recursion) #

Récursivité croisée #

Récursivité multiple #

Structures récursives #

Quelques erreurs “classiques” #

attention aux effets de bord #

oubli du return #

absence de prise de conscience de la localité des environnements #