pour impression

La cryptographie à clé publique - Principe de fonctionnement #

Dans les années 1970, la cryptographie n’est plus seulement l’apanage des militaires. Les banques notamment, pour la sécurité de leurs transactions, sont devenues de grandes consommatrices de messages cryptés. Les chiffres disponibles alors, comme le célèbre DES, sont sûrs, tout du moins en comparaison des moyens que l’on peut déployer à cette date pour les vaincre.

Ils sont sûrs, à condition que destinataire et expéditeur parviennent à échanger les clés de chiffrement. Les États ont recours aux valises diplomatiques pour ces échanges, mais ceci n’est pas accessible aux civils…

Protocole d’échange de clé de Diffie et Hellman #

  En 1976, Whitfield Diffie et Martin Hellman proposent une nouvelle façon de procéder, qui contourne cet écueil. Commençons par expliquer ceci de façon imagée. Un ami doit vous faire parvenir un message très important par la poste, mais vous n’avez pas confiance en votre facteur que vous soupçonnez d’ouvrir vos lettres.

Comment être sûr de recevoir ce message sans qu’il soit lu? #

  Vous commencez par envoyer à votre ami un cadenas sans sa clé, mais en position ouverte. Celui-ci glisse alors le message dans une boite qu’il ferme à l’aide du cadenas, puis il vous envoie cette boite. Le facteur ne peut pas ouvrir cette boite, puisque seul vous qui possédez la clé pouvez le faire.

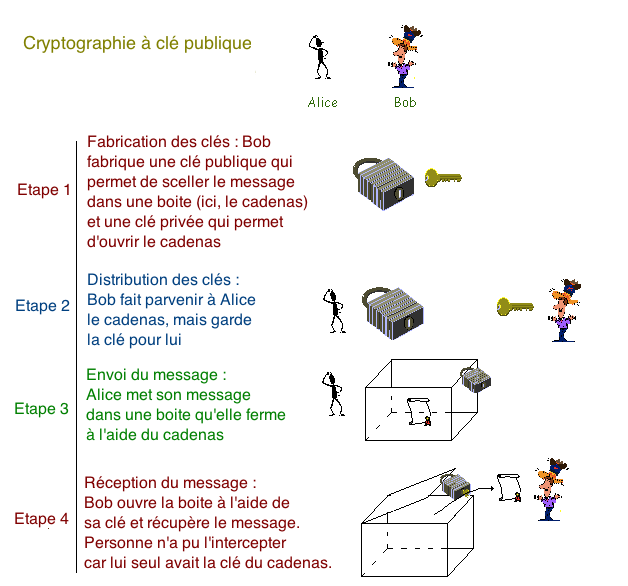
  La cryptographie à clé publique repose exactement sur ce principe. On dispose d’une fonction $P$ qui permet de chiffrer les messages. Ce procédé est inversible, c’est-à-dire que l’on dispose d’une fonction de déchiffrement $S$. On peut fabriquer simultanément un couple $(P,S)$, mais connaissant uniquement $P$, il est impossible (ou au moins très difficile) de retrouver $S$.

• $P$ est la clé publique (le cadenas), que vous pouvez révéler à quiconque. Si Louis veut vous envoyer un message, il vous transmet P(message).
• $S$ est la clé secrète (la clé du cadenas), elle reste en votre seule possession. Vous décodez le message en calculant $$S(P(\text{message}))=\text{message}.$$
• La connaissance de $P$ par un tiers ne compromet pas la sécurité de l’envoi des messages codés, puisqu’elle ne permet pas de retrouver S. Il est possible de donner librement $P$, qui mérite bien son nom de clé publique.

Un fonctions à sens unique ? #

  Bien sûr, il reste une difficulté : comment trouver de telles fonctions $P$ et $S$ ? Diffie et Hellman n’ont pas eux-même proposé de fonctions satisfaisantes, mais dès 1977, D. Rivest, A. Shamir et L. Adleman trouvent une solution possible, la meilleure et la plus utilisée à ce jour, la cryptographie RSA. Le RSA repose sur la dichotomie suivante :

• il est facile de fabriquer de grands nombres premiers $p$ et $q$ (pour fixer les idées, 500 chiffres).
• étant donné un nombre entier $n=pq$ produit de 2 grands nombres premiers, il est très difficile de retrouver les facteurs $p$ et $q$.

  La donnée de $n$ est la clé publique : elle suffit pour chiffrer. Pour déchiffrer, il faut connaître $p$ et $q$, qui constituent la clé privée. Le problème de factorisation de grands entiers étant très difficile, la connaissance de la clé publique $n$ ne permet pas de retrouver les entiers $p$ et $q$, qui constituent la clé secrète.

En pratique : combiner chiffrement symétrique et asymétrique #

  Cela dit, les algorithmes à clé publique (on parle aussi de chiffrement asymétrique) sont rarement utilisés pour chiffrer complètement un long message. Ils sont en effet très lents, beaucoup plus lents que leurs homologues symétriques. Pour des applications où il faut échanger de nombreuses données, ils sont inutilisables en pratique. On a alors recours à des cryptosystèmes hybrides. On choisit un chiffre symétrique (AES,…) pour l’échange du message. La cryptographie à clé publique est alors utilisée pour l’échange de la clé de ce chiffrement symétrique. De nombreux protocoles utilisés en pratique (protocole SSL pour le commerce électronique, logiciel PGP pour le courrier électronique) fonctionnent sur ce principe.

Chiffrement symétrique et asymétrique : une sécurité différente #

  Signalons aussi une différence essentielle entre la sécurité des chiffres asymétriques (RSA,…) et la sécurité des chiffres symétriques (AES,…).

• La sécurité de ces derniers repose simplement sur des idées heuristiques. On a suffisamment bien compliqué le message, on l’a suffisamment rendu “aléatoire” pour qu’il soit indéchiffrable pour qui ne connaît pas la clé.

• Pour les chiffres asymétriques, la sécurité repose sur des problèmes mathématiques bien particuliers dont on pense qu’ils sont difficiles à résoudre (factoriser des entiers, trouver un logarithme dans un groupe discret,….). Il y a finalement très peu d’algorithmes à clé publique différents, car on connaît très peu de problèmes de ce genre.

  Une grande avancée théorique (comme la découverte d’un algorithme de factorisation rapide), pourrait mettre à mal la sécurité de tous les chiffres à clé publique basés sur le RSA par exemple.