Fonctions exponentielles #
1. Définition & propriétés #
Introduction #
On considère la suite géométrique de raison $a$, définie par $u_n=a^n$. Elle est définie pour tout $n \in \mathbb{N}$. On peut prolonger son ensemble de définition à $\mathbb{R}$ tout entier avec $f(x)=a^x$.
On peut ainsi donner une image à des nombres non entiers comme 3.5.
Définition #
La fonction $f,$ définie sur $\mathbb{R}$ avec $a>0$ par $f(x) = a^x$ est la fonction exponentielle de base $a$.
Exemple #
Propriétés algébriques #
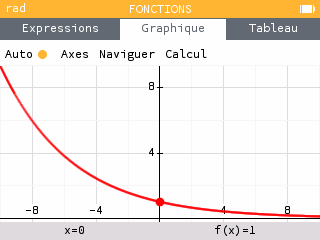
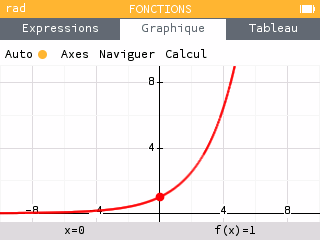
La fonction exponentielle de base $a$ est toujours positive.
Pour tout $x$ dans $\mathbb{R}$, $a^{-x}=\dfrac{1}{a^x}$.
$a^0 = 1$, $a^1=a$
$a^{x+y} = a^x \times a^y$
$a^{x-y} = \dfrac{a^x}{a^y}$
$(a^{x})^y = a^{xy}$
2. Variations #
Si $0 < a < 1$, $x \mapsto a^x$ est décroissante sur $\mathbb{R}$ #
Si $a > 1$, $x \mapsto a^x$ est croissante sur $\mathbb{R}$ #
3. Utiliser une fonction exponentielle #
Hz. capitale du monde #
La population d’Hz. ne cesse de croitre ! La qualité indéniable de son lycée en fait une des villes les plus attractives du monde.
Suite à des relevés très précis, le maire décide de modéliser la population d’Hz. avec la fonction exponentielle $f(x) = 30000 \times 1.3^x$ où $x$ est le nombre d’année après 2020.
- Quel est le sens de variation de la population d’après ce modèle ?
- Calculer la population d’Hz. en 2021, en 2022
- Calculer les valeurs successives jusqu’à dépasser $100
000$ habitants puis $1000~000$
-
La fonction exponentielle de base 1.3 est croissante, multiplier par $30~000$ ne change pas les variations donc la population est croissante.
-
En 2021, la population d’Hz. s’élève à $f(1) = 30000 \times 1.3^1 = 39000$
En 2022, la population s’élève à $f(2) = 30000 \times 1.3^2 = 50700$
-
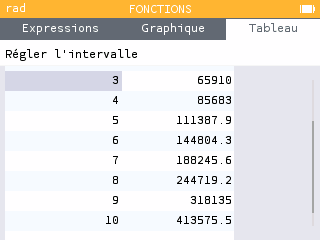
En zappant quelques valeurs intermédiaires on a :
$x$ $f(x)$ 4 $85~683$ 5 $111~388$ … … 13 $908~626$ 14 $1 181213$La population d’Hz. dépassera $100~000$ en 2025 et un million en $2034$.
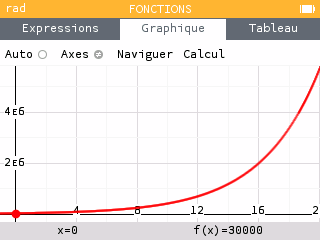
Ce modèle, totalement irréaliste, illustre une propriété de la fonction exponentielle de base $a>1$ : elle explose rapidement vers l’infini !
Les bactéries inarrêtables #
Le nombre de bactéries présentes dans un organisme suite à une infection est modélisé par $f(x) = 50000 \times 1.5^x$ où $x$ est en heures.
- Donner un arrondi au millier du nombre de bactéries après 30 minutes et après 1h30
- Déterminer les variations de $f$ sur [0; 10]
- Déterminer le temps nécessaire pour que la population double.
Après 30 minutes, soit 0.5 heures, le nombre de bactéries est $f(0.5) = 61000$ environ. Après 1h30, soit 1.5 heures, le nombre de bactéries et de $f(1.5) = 92000$ environ. La fonction exponentielle de base $1.5$ est croissante donc $f$ aussi. On a remarqué que $f(1.5)$ est presque le double de 50000. Essayons $f(2) = 111000$ environ et $f(1.71) = 100000$ environ. Il faut donc 1.7 heures = 1h et $0.7 \times 60$ minutes, soit 1h42 pour doubler la population (environ…)
4. Taux d’évolution moyen #
Les fonctions exponentielles permettent de modéliser facilement des accélérations.
Exemple #
Entre 2012 et 2015, le prix du gaz a augmenté de 25%. Calculer le taux d’évolution annuel moyen.
Notons $t$ ce taux, le coefficient multiplicateur d’une augmentation annuelle est $1 + \dfrac{t}{100}$.
Le coefficient multiplicateur de trois augmentations successives est
$$\left(1+\dfrac{t}{100}\right)\left(1+\dfrac{t}{100}\right)\left(1+\dfrac{t}{100}\right) = \left(1+\dfrac{t}{100}\right)^3$$
Une augmentation de 25% correspond à un coefficient multiplicateur de 1.25 donc on peut poser une équation :
$$\left(1+\dfrac{t}{100}\right)^3 = 1.25 \Longleftrightarrow 1 + \dfrac{t}{100} = 1.25^{\frac{1}{3}}$$ $$\Longleftrightarrow \dfrac{t}{100} = 1.25^{\frac{1}{3}} - 1 \Longleftrightarrow t = 100 \times (1.25^{\frac{1}{3}} - 1)$$ $$\Longleftrightarrow t \approx 7.72%$$
Le prix du gaz a augmenté d’environ $7.72%$ par an entre 2012 et 2015.
Remarque #
On a utilisé la formule suivante :
Pour tout $a>0$ et $x>0$, on a $a^n=x \Longleftrightarrow a = x^{\frac{1}{n}}$
$x^{\frac{1}{n}}$ est la racine énième de $x$.