Suites arithmétiques #
Rappels #
Suite #
Une suite numérique est une collection numérotée de nombres.
L’indice d’un élément de la suite est un entier, le premier indice est généralement 0.
Ainsi, la suite des entiers naturels pairs : $0, 2, 4, 6$ etc. peut être notée : $u_0 = 0, u_1=2, u_3=4$ etc.
Ou plus simplement : $u_n = 2n$.
Suite arithmétique #
Une suite est arithmétique si la différence de deux termes consécutifs est constante.
Lorsque c’est le cas, cette différence est appelée la raison de la suite et est notée $r$.

Définition #
Une suite $u$ est arithmétique de raison $r$ si, pour tout $n\in \mathbb{N}$, $u_{n+1} = u_n + r$.
Exemples #
- La suite $u$ définie par $u_0=4$ et $u_{n+1} = u_{n} + 5$ est arithmétique de raison 5.
- La suite $v$ définie par $v_0=5$ et $v_{n+1} = 2 v_{n}$ n’est pas arithmétique.
Méthodes #
Pour vérifier qu’une suite n’est pas arithmétique on se contente généralement de contredire la propriété sur les premiers termes.
Pour la suite $v$, $v_0=5, v_1=10, v_2=20$. Les différences successives sont : 5 (entre $v_0$ et $v_1$) et 10 (entre $v_1$ et $v_2$). $5 \neq 10$ donc la suite $v$ n’est pas arithmétique
Pour démontrer qu’une suite est arithmétique il faut le prouver pour un indice quelconque.
Considérons $w_n = 3 + 7n$. Prouvons que cette suite est arithmétique.
-
On exprime $w_{n+1}$ :
$w_{n+1} = 3 + 7(n+1) = 3 + 7n + 7 = 10 + 7n$
-
On calcule $w_{n+1} - w_n$ :
$w_{n+1} - w_{n} = (10 + 7n) - (3 + 7n) = 10 + 7n - 3 - 7n = 7$
-
Si la différence est constante (ne dépend pas de $n$), la suite est arithmétique. Sinon elle ne l’est pas.
7 ne dépend pas de $n$ donc $w_n$ est arithémtique de raison 7.
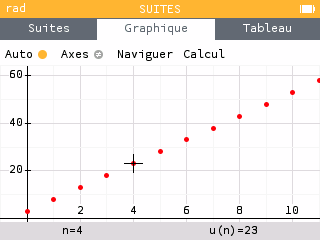
Graphiquement #
Les termes d’une suite arithmétique sont alignés. On parle de croissance linéaire
Lorsqu’on représente une suite on place en abscisse (horizontal) les indices et en ordonnée (vertical) les valeurs.
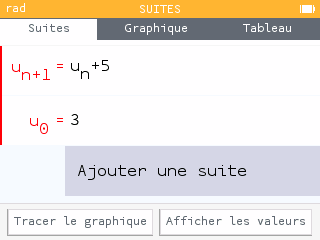
Représenter une suite sur la Numworks #
Lorsqu’on dispose de la relation $u_{n+1} = u_n + r$ :
Par exemple avec $u_3$ et $u_{n+1} = u_n + 5$.
Menu Suites, ajouter une suite, Récurrente d’ordre 1, $u_{n+1} = u_{n} + 5$
Ensuite graphique :
Variations #
Exprimer les variations d’une suite c’est dire si elle est croissante, décroissante ou ni l’un ni l’autre.
- Une suite arithmétique de raison $r>0$ est croissante.
- Une suite arithmétique de raison $r<0$ est décroissante.
Terme général #
Le terme général d’une suite est son expression en fonction de $n$
Le terme général d’une suite arithmétique est de la forme $u_n = u_0 + n \times r$

Somme des termes #
La somme des termes consécutifs d’une suite est la somme : $u_0 + u_1 + u_2 + \cdots + u_{n-1} + u_n$.
$u_0 + u_1 + u_2 + u_3$ : il y a 4 termes.
De l’indice 0 à l’indice $n$ il y a $n+1$ termes.
La somme des termes consécutifs d’une suite arithmétique #
$$S_n = u_0 + u_1+ u_2+ \cdots +u_n$$ $$S_n= \text{nb de termes} \times \frac{\text{1er} + \text{dernier terme}}{2}$$
Exemple #
On considère la suite $u$ donnée par $u_0=3$ et $u_{n+1} = u_n + 5$.
Calculer la somme $S = u_0 + u_1 + \cdots + u_{10}$
-
La suite est arithmétique de raison 5 donc la formule s’applique.
-
La somme s’étend de l’indice 0 à l’indice 10 donc comporte 11 termes.
-
Le dernier terme de la somme est $u_{10}$ qu’on calcule avec le terme général :
$$u_{10} = u_0 + 10 \times r = 3 + 10 \times 5 = 53$$
-
On remplace dans la formule :
$$S = 11 \times \dfrac{u_0 + u_{10}}{2} = 11 \times \dfrac{3 + 53}{2} = 11 \times \dfrac{56}{2} = 11 \times 28 = 308$$
Numworks #
Pour calculer la somme des termes avec la calculatrice Numworks il faut connaitre le terme général.
Menu calculs, touche paste, choisir Analyse puis Somme
$$\sum_{i=0}^{10}(3 + 5 \times i) = 308$$

Résumé #
| Résumé | Cours | Exemple |
|---|---|---|
| Définition | $(u_n)$ arithmétique – de raison $r$ – de premier terme $u_0$ | $r=-0.5$, $u_0=6$ |
| Propriété | $u_{n+1} = u_n + r$ | $u_{n+1} = u_n - 0.5$ |
| Propriété | $u_{n} = u_0 + n\times r$ | $u_{n} = 6 - 0.5r$ |
| Variations | Si $r>0$, $u$ est croissante – Si $r<0$, $u$ est décroissante | $r=-0.5$ – La suite est décroissante |
| Somme | $S = \text{nb de termes} \times \dfrac{\text{1er} + \text{dernier terme}}{2}$ | $u_2+\cdots+u_9 = 8\dfrac{u_2+u_8}{2}$ |
| Graphe | Les points de la représentation graphique sont alignés | |
| On parle de croissance linéaire | 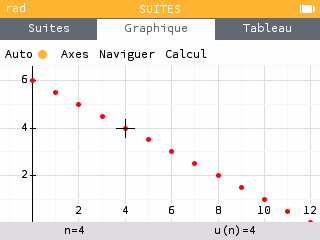 |