pdf: pour impression

Exercices sur les graphes #

Exercice 1 #

On considère le graphe suivant :

1. Est-ce un graphe simple ? orienté ?

2. Quels sont les voisins de $1$ ?

3. Construire sa matrice d’adjacence.

4. Combien peut-on ajouter d’arêtes à ce graphe ?

Exercice 2 #

Un graphe simple est dit complet si tous ses sommets sont reliés.

Ci-dessous les graphes complets $K_2$, $K_3$ et $K_4$.

1. Construire $K_5$ et $K_6$.
2. Construire les matrices d’adjacence de $K_2$, $K_3$, $K_4$.
3. Combient d’arêtes comportent-ils ?
4. En examinant les matrices d’adjacence, déterminer le nombre maximum d’arêtes d’un graphe comportant $n$ sommets.

Exercice 3 #

1. Déterminer tous les chemins élémentaires reliant $A$ à $D$

   • Un chemin d’origine $A$ et d’extremité $D$ est une suite d’arcs consécutifs reliant $A$ à $D$.
   • Un chemin est élémentaire s’il ne passe pas deux fois par le même sommet.

2. Déterminer tous les chemins simples reliant $A$ à $D$

   • Un chemin est simple s’il ne passe pas deux fois par le même arc.

3. Pour chaque sommet $y$, déterminer les autres sommets $x$ dont on peut partir pour atteindre $y$.

4. Quelles arêtes peut-on ajouter pour pouvoir relier n’importe quelle couple de sommets par un chemin ?

Exercice 3 #

\

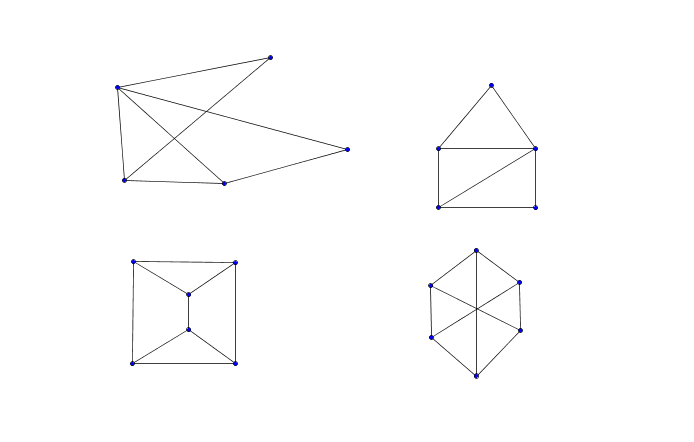Parmi les graphes ci-dessus lesquels représentent le même graphe ?