Cours

pdf

Programmation dynamique #

La programmation dynamique est une méthode algorithmique qui vise à résoudre des problèmes d’optimisation.

Le terme programmation est à comprendre dans le sens “planification et ordonnancement” pas dans le sens “écrire un programme dans un langage particulier”.

Voici un contexte dans lequel elle s’applique :

Programmation dynamique :

La programmation dynamique désigne une classe d’algorithmes qui résolvent un problème complexe en le divisant en sous-problèmes et en conservant les résultats des sous-problèmes pour éviter de calculer à nouveau les mêmes résultats.

Deux propriétés principales d’un problème suggèrent qu’il peut être résolu à l’aide de la programmation dynamique :

• Chevauchement de sous-problèmes
• Sous-structure optimale

Chevauchement de sous-problèmes #

Ce qu’on entend par là c’est le fait d’avoir à faire plusieurs fois le même calcul.

Afin d’illustrer ce principe, l’exemple classique est celui de la suite de Fibonnacci.

Suite de Fibonnacci :

• $F_0 = 0$
• $F_1 = 1$
• $F_{n + 2} = F_{n + 1} + F_{n}$ pour tout $n \in \mathbb{N}$

On veut simplement calculer le énième terme de la suite de Fibonnacci.

Pour calculer $F_4$ quels sont les termes dont on a besoin ?

Appliquons simplement la relation de récurrence jusqu’à atteindre les valeurs connues :

• $F_4 = F_3 + F_2$
• $F_3 = F_2 + F_1$
• $F_2 = F_1 + F_0$

Que peut-on déjà remarquer ?

1. Pour calculer $F_4 = F_3 + F_2$ on a besoin de $F_3$ et de $F_2$
2. Pour calculer $F_3 = F_2 + F_1$ on a besoin de $F_2$ et de $F_1$

On calcule donc deux fois la valeur $F_2$. Il serait bon de l’avoir conservée quelque part !

Implémenter cet algorithme avec cette relation de récurrence naïve conduit immédiatement à faire plusieurs fois le même calcul.

C’est un problème majeur.

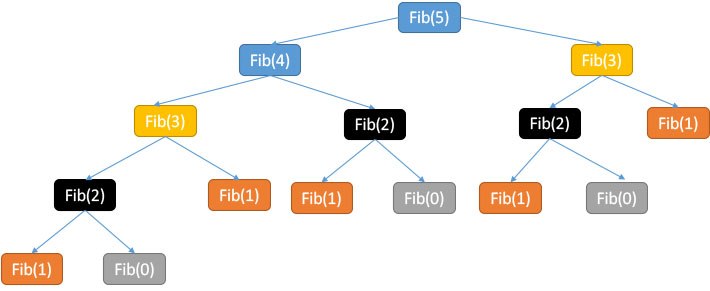
On peut s’en convaincre en regardant l’arbre des appels récursifs pour $F_5$

\

• En jaune : les deux fois où l’on appelle $F_3$
• En noir : les trois fois où l’on appelle $F_2$
• En orange : les cinq fois où l’on appelle $F_1$
• En gris : les trois fois où l’on appelle $F_0$

Ces résultats obtenus, il faut encore les ajouter ! C’est très long et particulièrement inefficace.

Chevauchement de sous-problèmes :

La programmation dynamique utilise la mémoïsation (noter l’orthographe particulière) pour résoudre le problème du chevauchement.

On conserve les résultats intermédiaires dans un tableau afin de remplacer un nouveau calcul par un appel mémoire

La complexité calculatoire est moindre mais l’espace mémoire est perdu.

Confusion avec “diviser pour régner”. #

Dans le chapitre “diviser pour régner” on a aussi vu qu’on pouvait examiner des sous problèmes…

Mais ceux-ci étaient indépendants.

Dans la dichotomie, par exemple, on choisit à chaque étape quel côté choisir. On ne traite pas à la fois le côté gauche et le côté droit.

Dans le cas de la programmation dynamique, on s’intéresse aux cas où les sous-problèmes se chevauchent.

• diviser pour régner : sous problèmes indépendants (ex. dichotomie)
• programmation dynamique : sous problèmes se chevauchent (ex. Fibonacci)

Sous-structure optimale #

Cela signifie qu’on peut découper le problème en sous-problèmes et les résoudre.

Les solutions des sous problèmes, une fois combinées donnent la solution du problème de départ.

Essayons d’illustrer avec un exemple : Geometry Dash.

Supposons quelques bricoles pour mieux comprendre :

1. Le joueur (vous ?) a une mémoire parfaite. Il se souvient de tout ce qu’il a déjà fait
2. Il est capable de reproduire ses faits et gestes sans erreurs depuis sa mémoire.
3. Il n’a jamais joué aux jeux-vidéos.

Retenu captif par un terrible kidnappeur, vous avez quatre jours pour terminer les quatre premiers niveaux de Geometry Dash.

• Le premier jour, après quelques tentatives, vous passez le premier niveau. Fier de votre exploit, vous vous arrêtez.
• Le second jour vous recommencez et, incroyable, ayant déjà franchi le premier niveau, vous n’avez aucune peine à vous souvenir de ce qu’il fallait faire. Vous refaites la même chose que lors de votre succès et entrez dans le second. Il est nouveau, vous n’en avez pas de souvenir. Néanmoins, doué comme vous l’êtes, vous le terminez rapidement et vous arrêtez.
• Le troisième jour, vous utilisez vos souvenirs du premier et du second vous franchissez le premier et le second niveau. À nouveau vous terminez le niveau en quelques essais.

Chacune de ces étapes présente bien une sous-structure optimale :

À chaque étape déjà rencontrée, le joueur refait la démarche qui lui a permis de réussir. Il ne refait pas les erreurs précédentes, il choisit immédiatement la meilleure approche.

Autrement dit, devant le nouveau problème “Atteindre le niveau 4”, il peut utiliser une sous-structure optimale : “Atteindre le niveau 3” qu’il a déjà réussie et dont il se souvient. Le seul nouveau problème qu’il rencontre alors est “Franchir le niveau 3”.

De même “Atteindre le niveau 3” utilise “Atteindre le niveau 2” et “Franchir le niveau 2” dont il se souvient.

Faisons varier un peu la contrainte.

Une fois libéré par vos kidnappeurs, c’est une autre équipe qui vous enlève. Moins intéressés par vos réflexes, ils vous confrontent au défi suivant : Vous devez tous les battre aux échecs consécutivement pour être libéré.

Vous pouvez essayer autant de fois que vous le souhaitez. La seule contrainte est d’enchaîner une victoire contre chacun d’entre eux.

Cette fois, il n’y a plus de sous-structure optimale :

Avoir battu Alfred aux échecs une fois ne vous assure pas d’une victoire dans une partie ultérieure.

Achevons de s’en convaincre :

Il y a bien une sous-structure…

• Pour sortir le joueur doit battre Alfred, Béatrice, Céline et Igor.
• Pour battre Igor, il doit avoir battu Alfred, Béatrice et Céline.
• Pour battre Céline il doit avoir battu Alfred et Béatrice.

Malheureusement, s’il reproduit ses coups à l’identique contre chacun de ces joueurs (comme lors de super Mario) il risque fort d’être déçu.

On imagine bien qu’un adversaire intelligent essayera d’éviter de reproduire une erreur.

Il suffit de joueur un nouveau coup rapidement pour que plus rien ne fonctionne.

Aussi retenir l’ensemble des coups de chaque partie peut-être utile mais n’est pas suffisant.

Conclusion : une sous structure est optimale si elle contribue à résoudre à coup sûr un problème plus difficile.

Approche du bas vers le haut #

Contrairement à la méthode diviser pour régner, la programmation dynamique privilégie une approche du bas vers le haut.

Dans l’exemple de Fibonacci, ça change tout !

Pour calculer $F_5$ on préfère calculer itérativement depuis les valeurs de départ plutôt que de reculer jusqu’à atteindre des valeurs connues.

En pratique comparons les deux algorithmes

Du haut vers le bas #

On utilise un tableau F[.] pour stocker les valeurs intermédiaires.

fonction fibonacci(n)
   si F[n] n'est pas défini
      si n = 0 ou n = 1
         F[n] := n
      sinon
         F[n] := fibonacci(n-1) + fibonacci(n-2)
   retourner F[n]

Du bas vers le haut #

fonction fibonacci(n)
   F[0] = 0
   F[1] = 1
   pour tout i de 2 à n
        F[i] := F[i-1] + F[i-2]
   retourner F[n]

Les deux approches sont bien de la programmation dynamique :

1. On utilise les sous problèmes (ici les valeurs déjà rencontrées),
2. Les sous problèmes se chevauchent,

Amélioration immédiate

La seconde approche peut-être rendue plus efficace en ne gardant en mémoire que les valeurs dont on a besoin.

On peut utiliser des variables plutôt qu’un tableau !

fonction fibonacci(n):
    x := 0
    y := 1
    Si n > 1:
    Pour tout k de 0 à n-1
      z := y
      y := x + y
      x := z
    retourner x

Cette nouvelle approche ne conserve que les derniers termes en mémoire, ceux dont on a réellement besoin.

Concevoir un algorithme #

La conception d’un algorithme de programmation dynamique est typiquement découpée en quatre étapes.

1. Caractériser la structure d’une solution optimale.
2. Définir (souvent de manière récursive) la valeur d’une solution optimale.
3. Calculer la valeur d’une solution optimale.
4. Construire une solution optimale à partir des informations calculées.

Remarque : La dernière étape est utile pour calculer une solution optimale, et pas seulement la valeur optimale. Un problème d’optimisation peut avoir de nombreuses solutions.

Chaque solution a une valeur, et on souhaite trouver une solution ayant la valeur optimale. Une telle solution optimale au problème n’est pas forcément unique, c’est sa valeur qui l’est.

Dans une ville il peut exister plusieurs trajets optimaux (en temps) reliant deux points :

1. Maison - Mairie - Salle des fêtes - Travail

   Durée : 10 minutes

2. Maison - Église - Terrain de sport - Maison hantée - Travail

   Durée : 10 minutes

La valeur optimale est alors 10 minutes mais il existe deux solutions optimales.