Resume

pdf : pour impression

Les graphes : une longue introduction #

Présentation #

La théorie des graphe est une théorie fondamentale de l’informatique et des mathématiques.

• le réseau routier d’un pays et le réseau de transport d’une ville forment un graphe :

• internet peut être pensé comme un graphe,

• les réseaux sociaux présentent naturellement des graphes entre les personnes,

Utilisation des graphes en informatique #

Parmi les problèmes fréquents faisant apparaître des graphes on rencontre :

1. La recherche des chemin. Puis-je passer de l’état $A$ à l’état $B$ ?

2. L’exploration de graphe.

3. La recherche de cycles dans un graphe.

4. Les algorithmes peuvent être vus comme des graphes :

Distinction mathématique, informatique #

Les définitions des graphes en mathématique et en informatique sont similaires. Les applications diffèrent souvent.

Nous (les informaticiens) cherchons souvent à exposer les solutions de nos problèmes. Un algorithme doit fournir une solution en un temps fini.

Objectifs #

Nous allons donc :

1. Définir une structure de donnée permettant de manipuler les graphes.

2. Implémenter cette structure.

3. Résoudre des problèmes utilisant les graphes et donc :

   • proposer des algorithmes pour les résoudre,
   • implémenter ces algorithmes.

Parmi les problèmes que nous allons aborder :

1. L’exploration de graphe,
2. La recherche de chemin dans un graphe,
3. La recherche de cycles dans un graphe.

Définitions #

Définition : Graphe simple #

Un graphe simple est un couple $G = (V, E)$ comprenant

• $V$ un ensemble de sommets (parfois appelés nœuds),

• $E$ un ensemble d’arêtes reliant ces sommets (parfois appelés arcs ou flèches).

  Une arrête est simplement un couple de sommets ou un ensemble de deux sommets.

Les termes et notations anglais, que vous rencontrerez souvent sont : sommet : vertice et arête : edge. D’où les noms des ensembles.

Exemple #

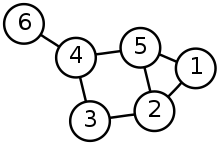
Dans le graphe ci-dessus

• Les sommets sont : $V = {1, 2, 3, 4, 5, 6}$
• Les arrêtes sont : $E = { {1, 2}, {1, 5}, {2, 3}, {2, 5}, {3, 4}, {3, 5}, {4, 5}, {5, 6}}$

Définition : Graphe orienté #

Lorsque les arêtes sont marquées d’une flèche, elles sont orientées.

Une arrête orientée ne se parcourt que dans le sens de la flèche. Dans ce cas on note généralement les arrêtes avec des parenthèses pour désigner des couples.

Par exemple l’arête $(1, 2)$ part de $1$ et arrive en $2$.

Structure de donnée graphe #

Introduction #

Il nous faut pouvoir représenter

• les sommets,
• les arrêtes.

Les sommets d’un graphe peuvent être enregistrés dans n’importe quelle “collection” :

• liste,
• tuples,
• dictionnaires,
• ensemble

Il existe plusieurs manières de décrire les arrêtes et toutes ont leur utilité.

Ensemble d’arêtes #

Par exemple : $G = (V, E)$ avec $V = {1, 2, 3, 4}$ et $E = {(1, 2), (2, 3), (3, 4), (2, 4)}$

Pour le graphe précédent avec un dictionnaire :

aretes = {
  1: [2],
  2: [1, 3, 4],
  3: [2, 4],
  4: [3, 2],
}

Matrice d’adjacence #

Définition :

Pour un graphe simple $G = (V, E)$ avec $n$ sommets, la matrice d’adjacence de $G$ est une matrice de dimension $n \times n$ dont l’élément $a_{ij}$ est 1 si les sommets $i$ et $j$ sont reliés par une arrête et 0 sinon.

Cette définition ne s’applique qu’aux graphes simples

Exemple :

Dans l’exemple du graphe ci-dessus, cela donne :

$$ \begin{pmatrix} 0 & 1 & 0 & 0\\ 1 & 0 & 1 & 1\\ 0 & 1 & 0 & 1\\ 0 & 1 & 1 & 0 \end{pmatrix} $$

Comment remplir la première ligne ?

• 1 n’est pas relié à 1 donc le premier nombre est 0.
• 1 est relié à 2 donc le second nombre est 1.
• 1 n’est pas relié à 3, le troisième nombre est 0.
• 1 n’est pas relié à 4, le quatrième nombre est 0.

On obtient bien la première ligne : $0\quad 1\quad 0\quad 0$.

Lorsque les sommets sont numérotés, il est naturel de choisir l’ordre correspondant, mais lorsque les sommets portent des noms (“Lille”, “Paris”, “Marseille”), l’ordre peut varier. On obtient alors une autre matrice d’adjacence qui lui est équivalente.

De la matrice d’adjacence à la représentation

Partant d’une matrice d’adjacence comme

$$ \begin{pmatrix} 0 & 1 & 1 & 1 & 0\\ 1 & 0 & 1 & 1 & 1\\ 1 & 1 & 0 & 1 & 0\\ 1 & 1 & 1 & 0 & 1\\ 0 & 1 & 0 & 1 & 0\\ \end{pmatrix} $$

Il existe un unique graphe qu’elle représente :

Remarque : attention cependant, si on change l’ordre des sommets on obtient une autre matrice d’adjacence ! La matrice d’adjacence est unique à l’ordre près des sommets.

Cas des graphes orientés #

Lorsque les graphes sont orientés on doit tenir compte de l’ordre.

Définition :

Dans le cas d’un graphe orienté, la matrice d’adjacence contient 1 à la ligne $i$, colonne $j$ s’il existe une arrête reliant le sommet $i$ au sommet $j$.

• Les lignes donnent les points de départ. La deuxième ligne de la matrice d’adjacence contient 1 pour chaque arête qui part de 2.

• Les colonnes donnent les points d’arrivée. La deuxième colonne de la matrice d’adjacence contient 1 pour chaque arête qui arrive en 2.

$$ \begin{pmatrix} 0 & 1 & 1 & 0\\ 0 & 0 & 0 & 1\\ 1 & 0 & 1 & 0\\ 0 & 0 & 1 & 0 \end{pmatrix} $$

Le graphe ci-dessus présente une boucle $3 \rightarrow 3$. Dans sa matrice d’adjacence on peut le voir parce qu’il y a un 1 sur la diagonale en $a_{3, 3}$

Structure de donnée graphe #

Primitives #

Quelles sont les primitives dont nous avons besoin pour créer un graphe ?

• créer un graphe (vide ou à partir d’une liste de sommets),
• ajouter un sommet,
• ajouter une arête,
• supprimer un sommet,
• supprimer une arête,
• le graphe est-il vide ?
• quels sont les sommets adjacents à un sommet donné ?

On peut aussi envisager :

• retourner la matrice d’adjacence d’un graphe,
• créer un graphe à partir d’une matrice d’adjacence.
• créer un graphe à partir de la liste de ses sommets (souvent appelée liste d’adjacence)

De nombreuses interfaces sont envisagéables. Certaines fonctionnent directement à partir des arêtes et créent les sommets dont elles ont besoin.

Les applications étant innombrables, pourra ajouter :

• fixer une valeur à une arête,
• retourner la valeur d’une arête,

ou

• fixer une valeur à un sommet,
• retourner la valeur d’un sommet.

Exemple #

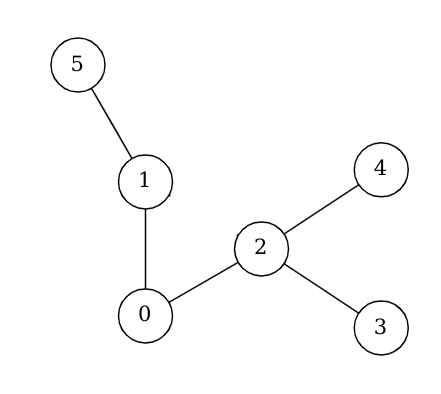
Pour le cas d’un graphe orienté, sans valeurs pour les sommets ni les arêtes, on peut illustrer :

>>> g = creer_graphe()
>>> g.est_vide()
True
>>> g.ajouter_sommet(1)
>>> g.est_vide()
False
>>> g.ajouter_sommet(2)
>>> g.ajouter_arete((1, 2)) # de 1 vers 2
>>> g.ajouter_arete((1, 3))
>>> g.ajouter_arete((3, 1)) # de 3 vers 1
>>> g.ajouter_arete((3, 2))
>>> g.voisins(1) # sommets qui accessibles depuis 1
[3, 2]
>>> g.voisins(2)
None
>>> g.matrice_adjacence()
[[0, 1, 1],
 [0, 0, 0],
 [1, 1, 0]]

Ce graphe est alors :

Algorithmes sur les graphes #

Algorithme : parcours en largeur dans un graphe simple #

source                              (un noeud du graphe)
file     : [Source]                 (une file)
drapeaux : [-1, -1, etc., -1]       (un tableau avec -1 pour chaque indice de
                                    sommet)

Dans le tableau drapeaux, si un sommet est d’indice 2,

drapeaux[2] = -1 signifie qu’on ne l’a pas encore ajouté à la file.
drapeaux[2] = 0 signifie qu’on l’a déjà ajouté à la file.

Parcours en largeur :

Changer le drapeau de la source à 0.

Tant que la file n'est pas vide faire :
    courant = défiler()
    Pour chaque voisin de courant qui n'a pas déjà été visité,
        l'ajouter à la file.
        Changer leurs drapeaux à 0.
    visiter courant. # c'est ici qu'on fera généralement un travail.

Exemple #

Disons que notre action “visiter” est d’afficher le numéro du sommet courant.

Sur le graphe précédent :

0. File = [0], drapeaux = [0, -1, -1, -1]
Début de la boucle.
1. On défile : courant = 0, File = []
    Voisins de 0 : 1 et 2 qu'on ajoute à la file. File = [1, 2]
      On change leurs drapeaux : drapeaux = [0, 0, 0, 1]
    On affiche 0
2. On défile, courant = 1. File = [2]
    voisins de 1 : 0, 2, 3. On ajoute 3 à la file (son drapeau vaut -1)
      File = [2, 3]
      On change le drapeau de 3 : drapeaux = [0, 0, 0, 0]
    On affiche 1
3. On défile, courant = 2, File = [3]
    voisins de 2 : 0, 1. Tous les drapaux valent 0, on n'ajoute aucun sommet.
    On affiche 2
4. On défile, courant = 3. File = []
    Tous les voisins de courant ont un drapeau valant 0.
    On affiche 3

La file est vide et la boucle est terminée.

L'affichage dans la console aura donné : 0, 1, 2, 3

C’est bien un parcours en largeur d’abord.

On explore tous les voisins avant d’avancer d’un niveau.

Algorithme : parcours en profondeur dans un graphe simple #

La seule différence est qu’on utilise une pile.

source                              (un noeud du graphe)
pile     : [Source]                 (une pile)
drapeaux : [-1, -1, etc., -1]       (un tableau avec -1 pour chaque indice de
                                    sommet)

drapeau = -1 : pas encore ajouté à la pile
drapeau = 0 : déjà ajouté à la pile

Parcours en profondeur :

Changer le drapeau de la source à 0.

Tant que la pile n'est pas vide faire :
    courant = dépiler()
    Pour chaque voisin de courant qui n'a pas déjà été visité,
        l'ajouter à la pile.
        Changer leurs drapeaux à 0.
    visiter courant. # c'est ici qu'on fera généralement un travail.

Exemple #

Sur le graphe précédent :

0. Pile = [0], drapeaux = [0, -1, -1, -1]
Début de la boucle.
1. On dépile : courant = 0, Pile = []
    Voisins de 0 : 1 et 2 qu'on ajoute à la pile. Pile = [1, 2]
      On change leurs drapeaux : drapeaux = [0, 0, 0, 1]
    On affiche 0
2. On dépile, courant = 1. Pile = [2]
    voisins de 1 : 0, 2, 3. On ajoute 3 à la pile (son drapeau vaut -1)
      Pile = [2, 3]
      On change le drapeau de 3 : drapeaux = [0, 0, 0, 0]
    On affiche 1

ATTENTION C'EST ICI QUE ÇA CHANGE : DÉPILER = SORTIR LE DERNIER

3. On dépile, courant = 3, Pile = [2]
    voisins de 3 : Tous les drapaux valent 0, on n'ajoute aucun sommet.
    On affiche 3
4. On dépile, courant = 2. Pile = []
    Tous les voisins de courant ont un drapeau valant 0.
    On affiche 2

La pile est vide et la boucle est terminée.

L'affichage dans la console aura donné : 0, 1, 3, 2

C’est bien un parcours en profondeur d’abord.

On explore un chemin le plus profondément possible avant d’avancer.

Algorithme : détermination d’un chemin dans un graphe simple. #

Première étape : parcourir #

On entretien un dictionnaire des visites, qui permettra de construire un chemin

Fonction Parcours en profondeur(source, destination)

  prochains     = [source]              (une pile)
  prédécesseurs = {source: Vide}        (un dictionnaire)

  tant que la pile n'est pas vide :
    On dépile courant.
    pour chaque voisin de courant
      Si voisin n'est pas déjà dans le dictionnaire des prédécesseurs
          On l'ajoute au dictionnaire avec comme valeur "courant"
          prédécesseurs[voisin] = courant
          On empile "voisin" dans la pile des prochains

          Si courant == destination, on arrête la boucle.

  On retourne à la fin le dictionnaire des visites

Deuxième étape, créer le chemin depuis le dictionnaire des visites. #

Fonction créer un chemin (prédécesseurs, source, destination)
  Si destination n'est pas dans le dictionnaire prédécesseurs :
      il n'est pas possible d'atteindre la destination et on retourne None

  Sinon:
    on initialise le chemin DEPUIS LA FIN
    chemin = [destination]

    pred = destination
    Tant que pred != source :
      On attribue à predecesseur sa valeur dans le dictionnaire :
        pred = prédécesseurs[pred]

      on l'ajoute au DEBUT du chemin
      chemin = [pred] + chemin

  On retourne chemin

Recherche de la présence de cycle dans un graphe simple #

Un cycle est un chemin dont la source et la destination sont égales.

Par exemple le graphe ci-dessous contient un cycle [0, 1, 2] :

Si on enlève simplement l’arête entre (1, 2) on obtient un graphe qui n’a plus de cycle :

On souhaite créer une fonction qui réponde “Vrai” pour le premier graphe (il a un cycle) et “Faux” pour le second: il n’en a pas.

Algorithme : présence d’un cycle dans un graphe #

On utilise un parcours en largeur (en profondeur c’est pareil).

La différence est le tableau des drapeaux.

Cette fois, lorsqu’on dépile, on ajoute la règle suivante :

• lorsqu’on dépile un élément, on passe le drapeau à 1.

Et lorsqu’on cherche à empiler les voisins, on ajoute la règle suivante :

• si un voisin rencontré a un drapeau à 0, c’est qu’il y a un cycle.

Algorithme complet #

source                              (un noeud du graphe)
file     : [Source]                 (une file)
drapeaux : [-1, -1, etc., -1]       (un tableau avec -1 pour chaque indice de
                                    sommet)

Dans le tableau drapeaux, si un sommet est d’indice 2,

drapeaux[2] = -1 signifie qu’on ne l’a pas encore ajouté à la file.
drapeaux[2] = 0 signifie qu’on l’a déjà ajouté à la file mais pas encore visité.
drapeaux[2] = 1 signifie qu’on l’a déjà visité le sommet.

Parcours en largeur :

Fonction Contient un cycle (graphe)

Choisir un sommet (n'importe lequel) et l'ajouter à la file.

Tant que la file n'est pas vide faire :
    courant = défiler()
    passer le drapeau de courant à 1.

    Pour chaque voisin de courant :
      Si son drapeau vaut 0:
        On a déjà rencontré ce sommet ! Il y a un cycle.
        Cycle_present = Vrai
      Si son drapeau vaut -1 :
        l'ajouter à la file.
        Changer son drapeaux en 0.

Retourner Cycle_present

Remarque : si le drapeau du voisin vaut 1, inutile de repasser par là.