Représenter des entiers en machine : le système binaire #
pdf pour impression et diaporama
Binaire #
Différentes bases #
Dans la vie courante on utilise la base 10.
En informatique on rencontre d’autres manières de représenter les nombres :
- binaire
- complément à 2
- octal
- hexadécimal etc.
- nombres à virgules flottantes
Quand on creuse, c’est encore plus complexe. Par exemple le langage Rust utilise 14 types différents pour représenter les nombres !
Pourquoi autant ?
Définir plusieurs types permet d’économiser de l’espace mémoire :
u8est un type d’entiers positifs occupant 8 bits donc s’étant de 0 à $2^8 - 1 = 255$u64, la même chose mais de 0 à $2^{64} - 1$.i8cette fois on s’autorise des nombres négatifs, toujours sur 8 bits, de $-2^7=-128$ à $2^7 - 1 = 127$.- etc.
Cette complexité supplémentaire offre une connaissance précise de la représentation en mémoire.
En Python, par contre, on se situe beaucoup plus haut : les entiers n’ont pas de limite de taille et peuvent être positifs ou négatifs. Il est impossible de savoir précisemment comment un entier sera représenté en mémoire sans entrer dans les détails du code.
Système de représentation par position #
Qu’on utilise la base 10, 2, 8, 16 ou autre, on emploie toujours la numération par position.
Représentation par position : La position d’un chiffre définit la valeur associée à ce chiffre.
Numération par position #
Exemple : En base 10 :
$345 = 3\times100 + 4\times10 + 5 = 3\times 10^2 + 4\times10^1+5\times10^0$
Le $3$ de $345$ représente donc $300$, le $4$ représente $40$ etc. On a pourtant $3 < 4$…
En binaire, on a deux chiffres. Chaque chiffre est un bit (=binary digit).
$0b1101 = 1 \times 2^3 + 1\times 2^2 + 0\times2^1 + 1\times2^0 = 13$
Afin d’indiquer une représentation binaire on utilise $0b$ avant le nombre ou $_2$ après le nombre :
$0b$
Les puissances de 2 #
Les puissances de 10 c’est facile : 1, 10, 100, 1000 etc. mais celles de 2 demandent un effort.
| Exposant $n$ | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| $2^n$ | 1 | 2 | 4 | 8 | 16 | 32 | 64 | 128 | 256 | 512 | 1024 | 2048 | 4096 | 8192 | 16384 |
Conseil : retenez les par coeur en jouant à 2048.
Du binaire au décimal. #
Pour convertir un entier donné en binaire on le lit depuis la droite et on fait la somme.
$0b10011$ = 1 + 2 + 0 + 0 + 16 = 19.
Autre notation : $10011_2 = 19_{10}$
Autre exemple :
La représentation décimale de $0b101010$ est
$$1\times2^5+0\times2^4+1\times2^3+0\times2^2+1\times2^1+0\times2^0$$ $$=32+8+2$$ $$=42$$
Du décimal au binaire. #
Deux algorithmes majeurs.
- Facile à programmer : les divisions successives.
- Facile de tête : soustraire des puissances de 2.
Décimal au binaire avec les puissances de 2. #
Écrire 57 en base 2 (=donner sa représentation binaire).
-
$32<57<64$.
Donc on fait $57 = 32 + 25 = 2^5 + 25$. On a un chiffre 1 à la position 6.
-
$16<25<32$.
Donc on fait $25 = 16 + 9 = 2^4 + 9$. On a un chiffre 1 à la position 5.
-
$8<9<16$.
Donc on fait $9 = 8 + 1 = 2^3 + 1$. On a un chiffre 1 à la position 4.
-
$1=2^0$.
On peut s’arrêter dès qu’on atteint une puissance de 2. On a un chiffre 1 à la position 1.
$$57 = 0b111001$$
Autre exemple :
$$123 = 64 + 59 = 64 + 32 + 27$$ $$123 = 64 + 32 + 16 + 11$$ $$123 = 64 + 32 + 16 + 8 + 3$$ $$123 = 64 + 32 + 16 + 8 + 2 + 1$$
Donc
$$123 = 0b1111011$$

Du décimal au binaire avec les divisions successives #
Algorithme des divisions successives
- On divise par 2 jusqu’à ce que le quotient soit 0
- On lit les bits en montant de droite à gauche :
Donner la représentation binaire de 167.
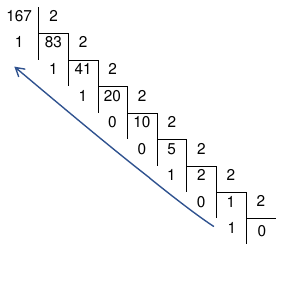
167 = 0b10100111
Exercice 1 #
-
Donnez les valeurs entières représentées par $0b0100$, $0b10101$, $0b101$, $0b0101$ et $0b00101$.
-
Comparez les valeurs entières représentées par $0b11$ et $0b100$, $0b111$ et $0b1000$.
Exercice 2 #
Quelle est la représentation binaire de 14 et 78 ?
Binaire en Python #
Python dérivant du langage C, les nombres en binaire sont notés 0bxxxx
Python converti naturellement un entier d’une base b vers le décimal avec int(nombre, b)
La conversion vers le binaire se fait avec bin et renvoie une chaîne de caractères.
>>> 0b111011
59
>>> a = '0b11'
>>> int(a, 2)
3
>>> b = 10
>>> bin(b)
'0b1010'
Faites bien attention :
0b111011est unintqu’on a écrit sous forme binaire et dont la valeur est 59."0b111011"est unestrqu’on peut convertir en entier avecint.
Les nombres en mémoire #
ATTENTION En mémoire, ce sont des entiers encodés en binaire.
>>> 4 + 5 9Ainsi, pour réaliser l’opération
4+5Python converti d’abord en binaire, additionne puis converti en décimal pour afficher9.
Taille d’un nombre en binaire #
Le nombre de bit d’un entier nous indique l’espace mémoire minimal qu’il faudra pour le stocker.
$123 = 0b1111011$ il faut au moins 7 bits pour stocker ce nombre.
En pratique, les machines utilisent des blocs de taille 1 octet, ce nombre entre dans un octet.
Taille et opérations #
Si $x$ occupe
nbits et $y$ occupepbits alors :
- SOMME : $x + y$ occupe au plus
max(n, p) + 1bits,- PRODUIT : $x \times y$ occupe au plus
n + pbits.
Nombre $x$ $y$ $x+y$ $x\times y$ Nombre de bits $n$ $p$ $\leq max(n, p) + 1$ $\leq n + p$
Le logarithme binaire #
En mathématique, la fonction $\ln$ pour logarithme népérien ou logarithme naturel est une fonction ayant d’importantes propriétés.
Rendue populaire par Napier, elle a permis de considérablement simplifier les calculs à la main.
Vous verrez en mathématiques qu’elle permet de transformer les produits en somme : $\ln (a \times b) = \ln a + \ln b$
Une de ses propriétés est de donner une mesure du nombre de chiffres d’un nombre dans une base :
Si $t$ est la taille de $x$ en base $b$ alors $$\frac{\ln(n)}{\ln(b)} \leq t < 1 + \frac{\ln(n)}{\ln(b)}$$
Pour nous, cela se traduit ainsi :
En notant $\log_2 (n) = \frac{\ln n}{\ln 2}$ et $\lceil x \rceil$ l’arrondi supérieur de $x$ :
Le nombre de bits d’un entier $n$ est $\lceil \log_2(x + 1) \rceil$.
Calcul booléen #
Booléen #
Le terme booléen vient du nom du mathématicien britannique George Boole. Il est le créateur de la logique moderne qui s’appuie sur l’algèbre qui porte désormais son nom : l’algèbre de Boole.
Un booléen est une donnée dont la valeur ne peut prendre que deux états, soit l’état vrai soit à l’état faux. On utilise également le bit pour représenter des booléens : ainsi un 0 représente la valeur faux et un 1 représente la valeur vrai.
Un booléen en informatique #
En python les booléens sont
FalseetTrue.Toute comparaison produit un booléen.
Par exemple, l’instruction
1==2s’évalue àFalse:>>> 1 == 2 False
Bien que le résultat soit faux, cette instruction est VALIDE.
Fonction qui renvoie un booléen #
On peut tout à fait retourner un booléen.
def est_majeur(age):
return age >= 18
Et quand on l’exécute :
>>> est_majeur(22)
True
Comment reconnaître un débutant ?
Il écrit des trucs comme ça :
def est_majeur(age):
if age >= 18:
return True
else:
return False
Affecter un booléen à une variable #
À nouveau, cela ne pose aucun problème.
>>> x = 9
>>> # imaginez ici 50 lignes de code
>>> comparaison = x == 3
>>> comparaison
False
Opérateurs booléens #
On définit sur ces valeurs booléennes trois opérations :
- la négation (le NON logique)
- la conjonction (le ET logique)
- la disjonction (le OU logique)
Ce ne sont pas les seules mais ces opérations sont suffisantes pour décrire toute l’algèbre de boole.
Le NON logique #
Le NON logique d’un booléen a se définit par :
NON a vaut VRAI si et seulement si a vaut FAUX.
| a | NON a |
|---|---|
| 0 | 1 |
| 1 | 0 |
Le ET logique #
Le ET logique entre deux booléens a et b se définit par :
a ET b vaut VRAI si et seulement si a vaut VRAI et b vaut VRAI.
| a | b | a ET b |
|---|---|---|
| 0 | 0 | 0 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 1 | 1 | 1 |
Le OU logique #
Le OU logique entre deux booléens a et b se définit par :
a OU b vaut VRAI si et seulement si a vaut VRAI ou b vaut VRAI.
| a | b | a OU b |
|---|---|---|
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 1 |
Équivalences #
Il est possible de définir l’opérateur OU logique à partir du NON logique et du ET logique.
En effet, si a et b sont des booléens alors
a OU b = NON ((NON a) ET (NON b)).
On peut utiliser les tables de vérités pour démontrer cette égalité.
Preuve #
On construit une table dans lesquelles les colonnes représentent les différentes sous-expressions dont nous avons besoin. Les contenus des colonnes sont construits en appliquant aux colonnes connues les tables de vérité connues définies ci-dessus.
Dans notre cas en plus de a, b, parmi les expressions utiles à notre calcul on trouve :
NON a, NON b.
Une fois la table remplie pour ces deux expressions on peut déterminer celle de l’expression
(NON a) ET (NON b) :
si on définit x=NON a et y= NON b,
alors (NON a) ET (NON b)=x ET y.
Table intermédiaire #
| a | b | NON a | NON b | (NON a) ET (NON b) |
|---|---|---|---|---|
| x | y | x ET y | ||
| 0 | 0 | 1 | 1 | 1 |
| 0 | 1 | 1 | 0 | 0 |
| 1 | 0 | 0 | 1 | 0 |
| 1 | 1 | 0 | 0 | 0 |
On complète alors la table avec les expressions : NON ((NON a) ET (NON b)) et (a OU b)
Table finale #
| a | b | (NON a) ET (NON b) | NON((NON a) ET (NON b)) | a OU b |
|---|---|---|---|---|
| (x ET y) = z | NON z | |||
| 0 | 0 | 1 | 0 | 0 |
| 0 | 1 | 0 | 1 | 1 |
| 1 | 0 | 0 | 1 | 1 |
| 1 | 1 | 0 | 1 | 1 |
L’égalité des contenus des deux dernières colonnes démontre l’équivalence des deux expressions.
Exercice 3 : a ET b #
-
Trouvez une expression équivalente à a ET b construite uniquement à partir des opérateurs NON et OU.
-
Démontrez que votre proposition est correcte à l’aide des tables de vérité.
Exercice 4 : Lois de Morgan #
-
Démontrez les règles de distributivité suivantes :
- a ET (b OU c) = (a ET b) OU (a ET c)
- a OU (b ET c) = (a OU b) ET (a OU c)
-
Démontrez les lois de Morgan :
- NON (a OU b) = (NON a) ET (NON b)
- NON (a ET b) = (NON a) OU (NON b)
OU exclusif #
| a | b | a XOR b |
|---|---|---|
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 0 |
On rencontre également défini l’opérateur OU-exclusif, également appelé XOR (pour “eXclusive OR”).
Exercice 5 : XOR à partir des premiers #
Démontrez l’équivalence :
a XOR b = (a ET (NON b))) OU ((NON a) ET b)
Opérateurs en taille quelconque #
On applique, bit par bit nos opérateurs usuels :
NOT bit à bit #
Chaque bit est inversé.
Sur 4 bits, NOT 7 = 8
NOT 0111
= 1000
ET bit à bit #
Sur 4 bits, 5 AND 3 = 1 :
0101
AND 0011
= 0001
OU bit à bit #
Sur 4 bits, 5 OR 3 = 7 :
0101
OR 0011
= 0111
XOR bit à bit #
Sur 4 bits, 5 XOR 3 = 6 :
0101
XOR 0011
= 0110
Opérateurs bits à bits en Python #
x & y # ET bit à bit (ampersand) x | y # OU bit à bit (tuyau) ~x # NON bit à bit (tilde) x ^ y # XOR bit à bit (accent circonflexe)
Par exemple, pour le XOR bit à bit
0 ^ 0 = 0
0 ^ 1 = 1
1 ^ 0 = 1
1 ^ 1 = 0
60 = 0b111100
30 = 0b011110
60 ^ 30 = 0b100010 # XOR bit à bit en colonne
0b100010 = 34
>>> 60 ^ 30
34
>>> bin(60 ^ 30)
'0b100010'
Décalages à gauche et à droite #
Il existe aussi deux opérations courantes lorsqu’on manipule des bits :
x << y # x décalé de y bits à gauche
x >> y # x décalé de y bits à droite
Par exemple
111 << 2 = 11100: décalage de 2 bits vers la gauche.101110 >> 3 = 101: décalage de 3 bits vers la droite (les bits trop à droite sont supprimés).
Ces opérations correspondent à des produits ou des divisions par 2 :
- décaler d’un bit vers la gauche c’est multiplier par 2,
- décaler d’un bit vers la droite c’est diviser (entièrement) par 2.
>>> (x << y) == x * 2 ** y
True
>>> (x >> y) == x // (2 ** y)
True
Un schéma electronique représentant un décalage à gauche
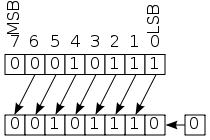
Exercice 6 #
- Calculez la représentation binaire de 29.
- Calculez la représentation binaire de 15.
- Démontrer que le ET bit à bit entre 29 et 15 vaut 13.
Les masques de sous-réseau #
Très largement inspiré de cet article de Wikipedia.
Les adresses IP de version 4, IPv4, sont codés sur 32 bits.
En notation décimale : 4 nombres compris entre 0 et 255, séparés par des points.
En fait, ce sont 4 octets généralement notés en décimal.
Par exemple : 192.168.100.2.
Elles sont ont composées de deux parties : le sous-réseau et l’hôte. Ils utilisent la même représentation.
On utilise des masques constitués (sous leur forme binaire) d’une suite de 1 suivis d’une suite de 0, il y a donc 32 masques réseau possibles.
Exemple de masque #
Un exemple possible est le masque 255.255.255.0.
Pour obtenir l’adresse du sous-réseau on applique l’opérateur ET entre les notations binaires de l’adresse IP et du masque de sous-réseau.
L’adresse de l’hôte à l’intérieur du sous-réseau est quant à elle obtenue en appliquant l’opérateur ET entre l’adresse IPv4 et la négation (NON) du masque.
Exercice 7 - Masques de sous-réseau #
- Calculez le code binaire correspondant à l’adresse
192.168.100.2 - Calculez le code binaire correspondant au masque
255.255.255.0. - Vérifier que l’adresse binaire du sous-réseau est
192.168.100.0 - Vérifier que l’adresse de l’hôte est
0.0.0.2
Conclusion : si le masque n’est constitué que de 255 et de 0 c’est facile.
Vers l’électronique et le calcul #
Électronique #
Représentation graphique #
A chaque porte est associée une représentation graphique. Voici pour les portes ET et XOR :
- porte ET

- Porte XOR

Portes logiques #
Les opérations logiques évoquées ci-dessus sont mises en oeuvre en électronique sous forme de portes logiques.
Les circuits électroniques calculent des fonctions logiques de l’algèbre de Boole.
Pour chacun des opérateurs logiques évoquées ci-dessus (et d’autres) il existe donc des portes logiques appelés porte ET, porte NON, etc. Les valeurs vrai et faux sont représentées par deux niveaux de tension, haut et bas.
Demi additionneur #
Un circuit de type porte ET dispose donc de deux entrées et une sortie.
La valeur du niveau de tension en sortie est obtenue avec la table de vérité du ET.
Les portes peuvent être connectées entre elles pour réaliser des circuits logiques et on peut ainsi réaliser des calculs.
Circuit du demi additionneur #

Il est appelé demi-additionneur car il réalise l’addition de 2 bits (A et B), le résultats de cette somme est représentée par S et la retenue éventuelle par R.
Exercice 8 - Étude du demi-additionneur #
Vérifiez, avec une table de vérité, que S et R correspondent bien aux valeurs de la somme et de la retenue sur 1 bit de A et B.
Un exemple plus élaboré, le circuit 7400 #
Circuit intégré 7400 contenant 4 portes NON-ET (NAND). Les deux autres broches servent à l’alimentation 0V / 5V.

Combinaisons plus complexes #
A partir de ce circuit on peut en construire d’autres plus complexes permettant d’additionner des nombres de plusieurs bits. Voir sur cette page par exemple.
Et on combine… jusqu’au micro-processeur qui réalise les calculs au sein d’un ordinateur. Il “suffit” de trouver la bonne organisation.
C’est un peu comme les Lego en somme… Vous pourrez trouver ici quelques compléments.
Nombres en binaires de plusieurs chiffres #
Comment ajouter rapidement deux nombres en binaire ?
$5 + 4 = 9$ donc $0b101 + 0b100 = 0b1001$
On part du dernier bit (de poids faible) et on compte les retenues.
Il suffit donc de deux portes logiques pour réaliser une addition sur un bit : le calcul du bit se fait par un XOR et la retenue par un AND.
Il serait intéressant, pour limiter le nombre de composants de pouvoir décaler les bits. Ainsi, en décalant à droite et en conservant les retenues, on aurait toujours affaire au bit de poids faible.