pdf

Représentation d’un texte en machine #

La mémoire ne contient que des 0 et des 1, ainsi lorsqu’on voit une lettre à l’écran, en mémoire c’est un entier qui encode ce caractère.

Différents encodages existent, nous allons les étudier.

Un caractère ? #

Comment enregistrer, de manière optimale, du texte en mémoire ?

De combien de symboles a-t-on besoin ?

• 26 lettres dans l’alphabet, 52 avec les majuscules.
• 10 chiffres 0123456789
• Un peu de ponctuation : ,;:!?./*$-+=()[]{}"' etc.
• Quelques caractères techniques (retour à la ligne, espace etc.)

On dépasse $2^6 = 64$ mais en se contentant du minimum, on reste en dessous de $2^7 = 128$. On peut encoder une table assez vaste avec 7 bits.

Idée d’ASCII (1961) : uniformiser les nombreux encodages incompatibles entre eux.

L’encodage ASCII est l’encodage universel dont tous les autres dérivent.

La table ASCII complète #

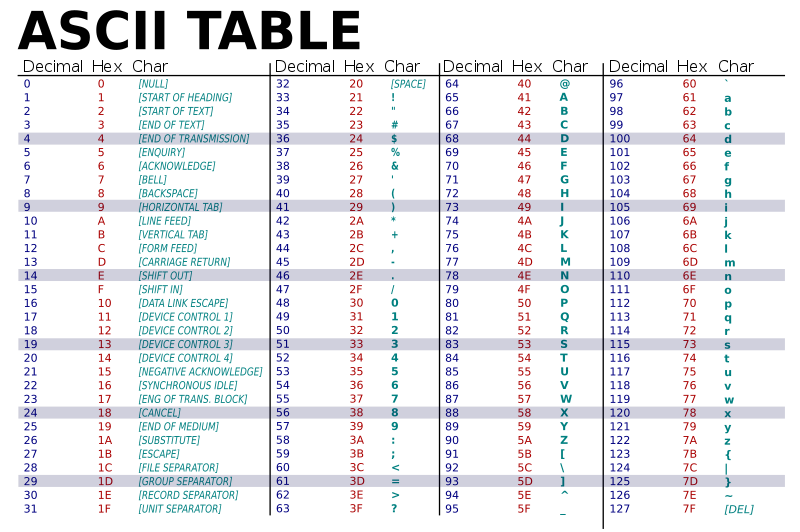
Remarques sur la table précédente #

• Tout élément de la table est codé sur 7 bits, 1 octet par caractère suffit
• Les caractères codés entre 32 et 127 sont imprimables, les autres sont des caractères de contrôle.
• Certains caractères de contrôle ont un effet sur le texte comme le numéro 9 : \t (tabulation) ou le 10 : \n (retour à la ligne).
• Les chiffres commencent à $30_{16}$, les majuscules à $41_{16}$ et les minuscules à $61_{16}$
• Pour obtenir la notation binaire, on part de l’hexa.
  Premier chiffre : 3 bits, second chiffre 4 bits $$A \rightarrow 41_{16} \rightarrow 4\times 16 + 1 \rightarrow 01000001$$ $$s \rightarrow 73_{16} \rightarrow 7\times 16 + 3 \rightarrow 01110011$$

Les 95 caractères imprimables #

• Seulement 95 caractères imprimables, pas de caractère accentués :

Question : Expliquer la phrase suivante : “Pour changer la casse d’un caractère, il suffit de changer 1 bit dans sa représentation ASCII.”

Résumé ASCII #

En ASCII on encode un caractère sur 7 bits.

Cet encodage ne comporte que 95 caractères imprimables (de 20 à 127) et aucun accent.

C’est le seul encodage “qui marche toujours”.

Si vous voyez un accent, ce n’est pas de l’ASCII.

L’organisation astucieuse permet de passer facilement de changer la casse.

Python et la table ascii #

Les fonctions chr et ord permettent d’accéder à la table

>>> chr(65) # caractère 65 (décimal)
'A'
>>> ord('A') # numéro décimal du caractère
65

Question : Comment reproduire la table ci-dessous en quelques lignes ?

 !"#$%&'()*+,-./0123456789:;<=>?
@ABCDEFGHIJKLMNOPQRSTUVWXYZ[\]^_
`abcdefghijklmnopqrstuvwxyz{|}~

for c in range(32, 128):
    if c and (c % 32) == 0:
        print()
    print(chr(c), end="")
print()

iso-8859-1 ou iso-Latin-1 #

Comment compléter la table ASCII ?

L’encodage iso-8859-1, dit iso-Latin-1 est apparu en 1986 et correspond à l’Europe de l’ouest. D’autres versions pour les caractères iso-Latin-2 de l’Europe de l’est etc.

• Reprend la table ascii et ajoute les accents au coût d’un bit supplémentaire (à gauche).

• Ainsi ASCII(A) = 0100 0001 = iso-latin1(A).

• Chaque caractère d’une table iso-xxxx-x occupe exactement 1 octet.

• Les caractères “spéciaux” commencent donc à 128 jusque 255.

• Encore incomplet : œ et Œ n’y sont pas ! Ce qui a contribué à leur disparition de nombreux documents écrits dans les années 90…

• Windows (Windows-1252) et Mac (MacRoman) ont leurs propres versions rendant l’échange de documents et développement de logiciels plus que pénibles.

Bref, c’est de la merde imparfait mais cet encodage étant encore la norme sous Windows, il faudra faire avec.

Unicode #

L’unicode et en particulier UTF-8 vise à résoudre TOUS les problèmes dans UNE norme.

• minimiser l’espace occupé par un caractère
• proposer un encodage adaptable à tous les caractères employés sur terre
• conserver l’ordre de la table ascii de départ

Unicode remonte à 1991, est encore en développement, comporte déjà 137 374 caractères d’une centaine d’écritures dont les idéogrammes, l’alphabet grec etc.

UTF-8 est utilisé par 90,5% des sites web en 2017 et dans la majorité des systèmes UNIX (comprenez les serveurs et appareils mobiles).

Motivation d’unicode : $ et £ #

Les machines des années 1980 étant fournies avec leur propre encodage, une somme d’argent en dollars se voyait attribuer le symbole monétaire $ aux USA et le symbole £ au Royaume Uni (symbole monétaire de la livre sterling).

Mais entre dollars ($) et livres (£) et les confusions étaient fréquentes.

Bob ---> Alice

> Je t'envoie 100$

Alice <--- Bob

> Je t'envoie 100£

On a ensuite, peu à peu, étendu ce projet à tous les symboles existant.

Principe simplifié d’UTF-8 #

• UTF-x n’utilise pas une taille fixe pour chaque caractère. Les plus courants occupent 1 bits.

• Chaque caractère est codé avec une séquence de 1 à 4 octets.

• Un texte encodé en ASCII est encodé de la même manière en UTF8 (sauf exception)

• Les premiers bits indiquent la taille de la séquence :

  • 0xxxxxxx : 1 octet
  • 110xxxxx 10xxxxxxxx : 2 octets
  • 1110xxxx 10xxxxxx 10xxxxxx : 3 octets
  • 11110xxx 1001xxxx 10xxxxxx 10xxxxxx : 4 octets

• Lorsqu’un document est encode en ASCII :

  • Si on lit un octet comme 0100 0001 on sait que c’est un caractère complet (A).
  • Lorsqu’il commence par 1110.... il faut lire les deux octets suivants pour connaître le caractère.

• On note U+XXXX un caractère encodé en UTF-8

• La taille est variable (génant pour les développeurs novices), l’espace en mémoire est parfois important

• Un caractère peut avoir plusieurs représentations $\rightarrow$ problèmes de sécurité informatique : certaines opérations interdites sont filtrées en reconnaissant des caractères. Ce problème est globalement résolu.

Python et l’UTF-8 #

Python 2 (l’ancien) et l’encodage des caractères #

Python 2 supporte bien UTF-8 à condition de lui demander.

Sans quoi le premier accent va faire planter python 2.

On trouve souvent dans l’entête d’un fichier .py :

#!/usr/bin/env python
# -*- coding: utf-8 -*-

qui signifient :

• Execute ce fichier avec python, situé dans le dossier /usr/bin/env
• l’encodage du fichier est en utf-8

Python 3 (le notre) #

Python 3 supporte nativement utf-8, on peut se passer de cette précision On utilise les fonctions chr et ord

• chr(entier) retourne le caractère encodé par cet entier en utf-8
• ord(caractère) retourne l’encodage utf-8 de ce caractère.

les fonctions chr et ord supportent unicode :) #

>>> chr(233)
'é'
>>> ord('é')
233
>>> ord('😽')
'128573'
>>> chr(128570)
'😺'

Martine écrit en UTF-8 #

WHAT ?

• La lettre é a été encodée en UTF-8 (parce que 2 caractères sont affichés)
  En mémoire elle occupe 2 octets (elle n’est pas dans la table ascii)
• Ces deux octets ont été décodés en iso-latin1 (1 octet par caractère), respectivement en

Complément : base64 #

Contexte #

L’email ne supporte que le texte. Afin de transmettre autre chose que du texte par email (images, vidéos, sons, dossiers compressés etc.) il convient de représenter le contenu du document sous la forme d’un texte.

Base 64 #

Base64 est l’encodage utilisé pour transmettre des pièces jointes par email. C’est un groupe de schéma pour encoder des données binaires sous forme d’un texte au format ASCII grâce à la représentation de ces données en base 64. Le terme base64 vient à l’origine de l’encodage utilisé pour transférer certains contenus MIME (Extensions multifonctions du courrier Internet).

base64 est aussi employé pour transmettre des du contenu dans les URL.

Principes de base 64 #

Cet encodage utilise 65 symboles de la table ASCII pour encoder 6 bits par un caractère.

Ce processus consiste à encoder 24 bits par une chaîne de 4 caractères.

On procède de gauche à droite, en concaténant 3 octets pour créer un seul groupement de 24 bits (8 bits par octet). Ils sont alors séparés en 4 nombres de seulement 6 bits ($2^6=64$ d’où le nom). Chacune des 4 valeurs est enfin représentée par un caractère de l’alphabet retenu.

   Valeur Codage         Valeur Codage         Valeur Codage         Valeur Codage
 0 000000 A           17 010001 R           34 100010 i           51 110011 z
 1 000001 B           18 010010 S           35 100011 j           52 110100 0
 2 000010 C           19 010011 T           36 100100 k           53 110101 1
 3 000011 D           20 010100 U           37 100101 l           54 110110 2
 4 000100 E           21 010101 V           38 100110 m           55 110111 3
 5 000101 F           22 010110 W           39 100111 n           56 111000 4
 6 000110 G           23 010111 X           40 101000 o           57 111001 5
 7 000111 H           24 011000 Y           41 101001 p           58 111010 6
 8 001000 I           25 011001 Z           42 101010 q           59 111011 7
 9 001001 J           26 011010 a           43 101011 r           60 111100 8
10 001010 K           27 011011 b           44 101100 s           61 111101 9
11 001011 L           28 011100 c           45 101101 t           62 111110 +
12 001100 M           29 011101 d           46 101110 u           63 111111 /
13 001101 N           30 011110 e           47 101111 v
14 001110 O           31 011111 f           48 110000 w        (complément) =
15 001111 P           32 100000 g           49 110001 x
16 010000 Q           33 100001 h           50 110010 y

La description complète est disponible ici

Remarques #

• Ce codage augmente la taille des données : la taille des données est augmentée d’au moins un tiers. Les caractères “blancs” (espace, tabulation, retour à la ligne) augmentent encore plus la taille.

  Avec ce codage, même les caractères lisibles dans les données d’origine sont encodés de manière illisible.

• L’intérêt de l’encodage base64 ne se trouve donc pas dans la représentation de données textuelles, mais surtout dans la représentation de données binaires.

  Lorsque l’on veut représenter des données binaires (une image, un exécutable) dans un document textuel, tel qu’un courriel, la transcription hexadécimale en ASCII des octets multiplierait la taille par deux, l’encodage en base64 permet de limiter cette augmentation.

  Par ailleurs, le reproche fait sur la lisibilité des données tombe de lui-même dans ces conditions : les données binaires n’ont pas vocation à être compréhensibles sans interprétation par un logiciel dédié (cas d’une image, par exemple).

Exemple #

Prenons le groupe de 3 caractères ASCII “Hi!”. Ci-dessous la première ligne indique en binaire l’équivalence de ces 3 octets. La transformation consiste comme on peut le voir, à séparer les bits pour former en sortie 4 groupes de 6 bits :

 8 bits   8 bits   8 bits  <=> 6 bits 6 bits 6 bits 6 bits
    H       i        !
01001000 01101001 00100001 <=> 010010 000110 100100 100001
                                 S      G      k      h

Les 4 groupes de 6 bits en sortie nous donnent les valeurs 18, 6, 36 et 33. Ainsi en suivant la correspondance de la table indexée nous obtenons les 4 caractères “SGkh”

Avec la commande base64 sous Linux :

$ echo -n 'Hi!' | base64

SGkh

Et pour décoder :

$ echo -n 'SGkh' | base64 -d
Hi!

>>> import base64
>>> base64.b64encode(b'Hi!')
b'SGkh'
>>> base64.b64decode(b'SGkh')
b'Hi!'
>>>

Si nous prenons une chaine de caractères qui n’a pas un nombre de bits multiple de 24, on complète avec un ou deux symboles =. Par exemple la chaîne “Salut” :

S        a        l        u        t
01010011 01100001 01101100 01110101 01110100
010100 110110 000101 101100 011101 010111 010000 ?????? (nombre de bits multiple de 24)
U      2      F      s      d      X      Q      =