Compléments algorithmique #

Recherche dichotomique #

$x$ est-il un élément de ma $liste$ ? #

On considère une liste de nombres rangés par ordre croissant

Ex : $l = [0, 1, 5, 17]$.

On cherche à savoir si un nombre y figure.

Solutions natives en Python #

Python le fait nativement :

>>> l = [0, 1, 5, 17]
>>> 5 in l, 8 in l
(True, False)

>>> l.index(5), l.index(8)
(2, -1)
# 5 est l'élément d'indice 2,
# 8 n'est pas dans la lsite

Oui mais comment ?

solution naïve #

On parcoure les éléments :

Pour i allant de 0 à la longueur -1 {
  si l[i] vaut 5 {
    renvoyer Vrai
  }
}
Renvoyer Faux

En python :

def Recherche(l, x):
  for i in range(len(l)):
    if l[i] == x:
      return i
  return -1 # x n'est pas dedans

Dans le pire des cas, on parcourt tout le tableau.

Recherche dichotomique #

Disons qu’on cherche 5.

On regarde l’élément central $m$.
- Si $m = 5$ c’est gagné. On renvoie sa position.
- Sinon, si $m > 5$ alors $5$ est à sa gauche.
  
  notre nouvelle liste est constituée des éléments à gauche de $m$
- Sinon, c’est que $5$ est à droite de $m$.
  
  notre nouvelle liste est constituée des éléments à droite de $m$
On recommence depuis le départ avec la nouvelle liste.

Exercice #

Proposer un algorithme en pseudo code avec une boucle tant que.
Compter les nombre maximal d’étapes pour une liste de taille 16, 32, 64 etc.
Que remarque-t-on ?
Coder cet algorithme en Python

Solution - pseudo code #

rechercheDicho(liste, clé){
  bas = 0
  haut = longueur(liste) - 1
  Tant que (bas < haut){
    med = (bas + haut) // 2
    si clé == liste[med] {bas = med ; haut = med}
    Sinon{
      si clé > liste[med] {bas = med + 1}
      sinon {haut = med - 1}
    }
  }
  si cle == liste[bas]{renvoyer Vrai}
  sinon {renvoyer Faux}
}

Solution (suite) #

Le pire des cas est atteint quand la clé n’est pas dans la liste.
Alors, on divise par $2$ la taille de la liste jusqu’à ce que sa taille soit 1.
S’il y a $r$ division, alors $2^r < n < 2^{r+1}$
On note $r \leq \log_2(n)$ - le logarithme évoqué plus tôt…
La recherche dichotomique est un algorithme en $O(\log_2 n)$
Pour une taille ~1000, la recherche séquentielle effectue au pire 1000 étapes,

la recherche dichotomique au pire 10.

Solution en python (P. Tutor) #

def rechercheDicho(liste, cle):
    bas = 0
    haut = len(liste) - 1
    while bas < haut:
        med = (bas + haut) // 2
        if cle == liste[med]:
            bas = med
            haut = med
        else:
            if cle > liste[med]:
                bas = med + 1
            else:
                haut = med - 1
    if cle == liste[bas]:
        return True
    else:
        return False

Algorithmes gloutons #

Les algorithmes gloutons (greedy) #

Classe d’algorithme qui font, étape par étape, un choix optimum local.

On cherche à optimiser une réponse selon un critère.

Le problème du sac à dos #

Un voleur, parvenu dans le coffre doit choisir comment remplir son sac pour dérober un maximum.

Il peut porter 50 kg.

Il cherche à le remplir pour optimiser le montant dévalisé.

Oui mais comment choisir ?

Algorithme glouton #

La solution simple consiste à remplir son sac en prenant toujours en premier l’objet de plus grande valeur qui entre dans le sac.

Sac à dos : glouton, exemple #

Poids : 1, 2, 4. Capacité du sac : 5

Toutes les valeurs sont égales aux poids.

On commence par 4.

4 $\leq$ 5 donc on prend 4. Il reste 1
On continue avec 2.

2 > 1 on ne prend pas 2.
On continue avec 1. $1 \leq 1$ donc on prend 1. Il reste 0. Terminé.

$5 = 1 \times 4 + 0 \times 2 + 1 \times 1$

Est-ce le meilleur algorithme ? #

NON !

Par exemple :

3 objets dans le coffre, capacité du sac : 5

Objet A : masse 4
Objet B : masse 3
Objet C : masse 2

L’algorithme glouton va choisir l’objet A (valeur la plus élevée) et s’arrêter.

La solution optimale est de prendre les objets B et C.

3 objets et ça échoue déjà !

Algorithme glouton : inutile ? #

Pas du tout ! Il existe un cas simple dans lequel il donne toujours la meilleure réponse :

suite super croissante : #

Les poids sont super croissants si, une fois triés, la somme des $k$ premiers est inférieure au poids $k+1$.
$1,~3,~5,~10,~21$ est une suite de poids super croissante.

$1 < 3 ;, 1 + 3 < 5 ;, 1 + 3 + 5 < 10$ etc.
$2,~3,~4$ n’en est pas une : $2+3>4$
Dans le cas “super croissant”, l’algorithme glouton rend toujours la combinaison optimale.

Sac à dos : un problème fréquent #

On retrouve ce problème un peu partout :

Gestion de portefeuille en finance : quelles actions choisir ?
Chargement d’avions : tous les bagages doivent être amenés, sans surcharge
Découpe des matériaux : réaliser un maximum de pièces en limitant les chutes

Sac à dos : un problème $NP$-complet #

On dit d’un problème informatique qu’il est de classe $P$ s’il existe un algorithme “polynomial” (en $n^2$, $n^8$ etc) qui renvoie une solution.
Il est $NP$ si on peut vérifier les solutions de manière polynomiale mais qu’il n’existe pas de moyen de les obtenir qui soit polynomiale.

Autrement dit : NP-complet = facile à vérifier, quasi impossible à résoudre.

L’algorithme du sac à dos est NP-complet. Il n’existe aucun algorithme “rapide” qui renvoie toujours la meilleure solution. On peut toujours la vérifier (il suffit d’ajouter les poids)

Recherche d’une solution #

Si l’algorithme glouton ne donne pas la meilleure solution, comment faire ?

Une solution naïve consiste à explorer toutes les combinaisons possibles.

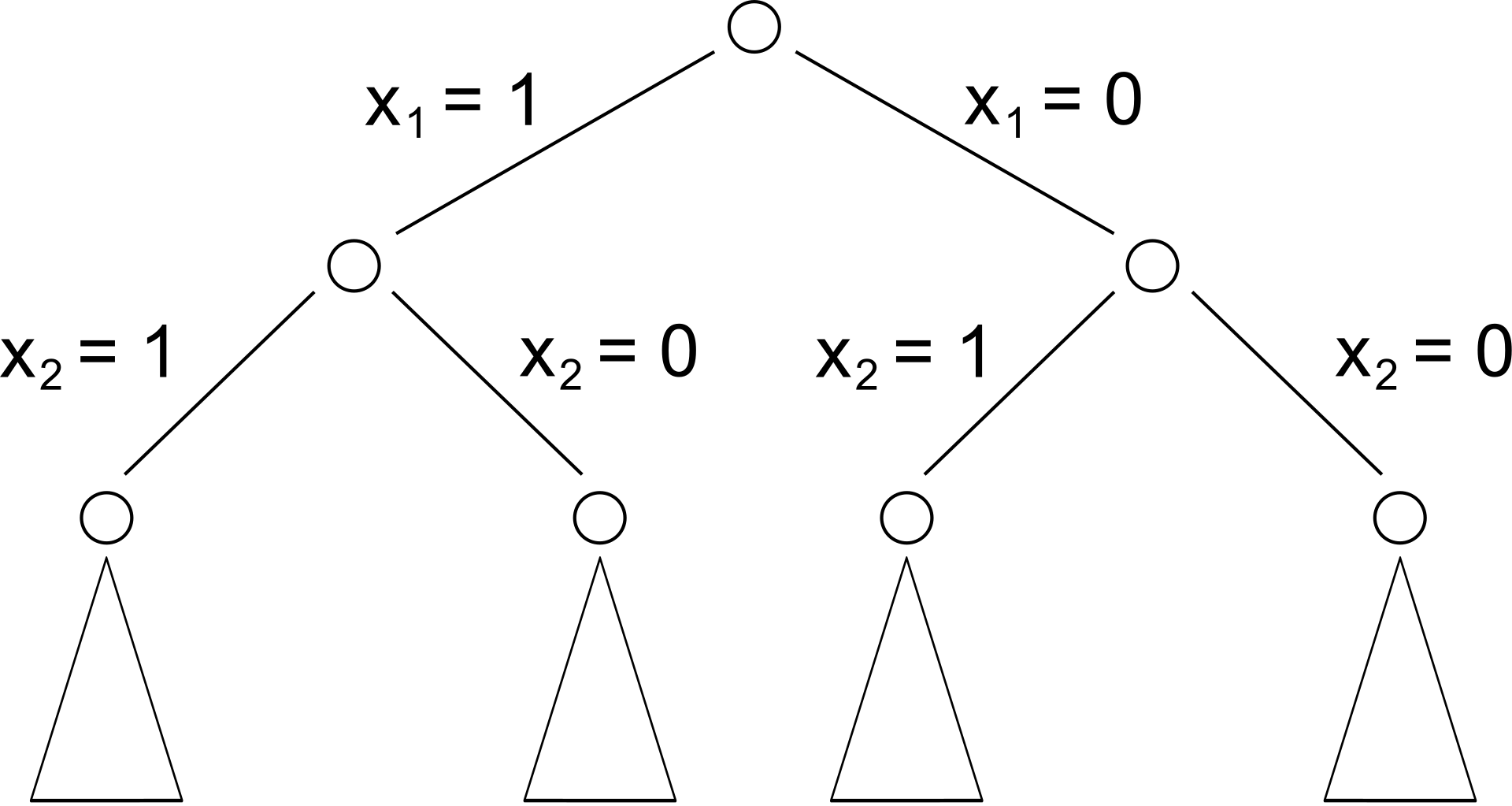
Arbre binaire #

rond : un poids, branche : une décision, triangle : un “sous-arbre”
$x_1 = 1$ je prends le poids 1. $x_1 = 0$, je ne le prends pas.
On note le poids total dans le rond et on explore le tout.

Arbre d’exploration binaire \

coût exponentiel #

À chaque fois qu’un objet est ajouté à la liste des objets disponibles, un niveau s’ajoute à l’arbre d’exploration binaire, et le nombre de cases est multiplié par 2.
L’exploration de l’arbre et le remplissage des cases ont donc un coût qui croît exponentiellement avec le nombre n d’objets.
100 objets, $2^{100}$ solutions possibles…

$2^{100} = 1267650600228229401496703205376$

$P = NP$ ? #

Voilà une des questions à 1 million de $ du Clay Institute

Y répondre par l’affirmative (et donner les algorithmes polynomiaux…) changerait l’informatique actuelle. En particulier, la cryptographie qui repose essentiellement sur la difficulté qu’ont les machines à trouver des solutions et la grande simplicité qu’elles ont à les vérifier

Donner deux entiers $p$ et $q$ tels que $p \times q = N$ avec $N = 60.186.563$.

Vous avez 10 secondes…

Cryptographie #

$60.186.563 = 7.757 \times 7.759$

Comment le sais-je ? Et bien c’est facile je suis parti de $p=7757$ et $q=7759$…

Ce sont deux nombres premiers (leurs diviseurs sont 1 et eux mêmes).
Maintenant imaginez que $p$ et $q$ comportent 100 chiffres.

Clé publique, clé privée #

A et B (les gentils) doivent s’envoyer un message privé
C (le méchant) veut lire le message.
Un des (nombreux) procédés pour échanger des messages chiffrés repose sur les nombres premiers :
- Facile de vérifier $p \times q = N$,
- Difficile de trouver $p$ et $q$ avec seulement $N$.
Il consiste à encoder un message avec la paire de clés $p$ et $q$ (qui sont très grands !). Ce sont les clés privées.
A et B connaissent ces clés privées, ils n’ont pas de mal à chiffrer et déchiffrer.
Le message qui transite sur le réseau, intercepté par C, ne fait apparaître que le nombre $N$ (la clé publique).
Mais, pour le déchiffrer, il doit connaître $p$ et $q$.

Il parviendra à factoriser, mais peut-être en 2000 ans…

Ça sert à quelque chose tout ça ? #

C’est le fondement des échanges sur internet et donc de l’économie moderne.

Achat en ligne, services bancaires, e mail, chat, streaming… sont (ou devraient…) être sécurisés.

Un pirate n’a aucun mal à intercepter le flux de données. Mais, si celui-ci est convenablement chiffré, il ne peut rien en faire.

Et ça fonctionne ? #

Oui… mais…

Oui, ça fonctionne. Si vous envoyez via une messagerie sécurisée un message à votre voisin(e), personne ne pourra le lire.
Mais il existe des entrées dérobées dans certains algorithmes. Et aussi des lois qui limitent la taillé des clés privées afin de laisser aux états la possibilité d’accéder aux contenus sensibles si nécessaire.
Exemple : en 2015 le FBI a cherché pendant 6 mois à déverrouiller un iPhone 5C. Apple refusait de le faire (mais pouvait le faire) et le FBI a dû trouver un ingénieur compétent autrement.

Entrée dérobée ? #

C’est un moyen de contourner le problème brutal “trouver $p$ et $q$ tels que $N = p \times q$” et de déchiffrer l’information directement. Certains algorithmes en ont dès leur conception.
Parfois c’est l’implémentation du programme qui en laisse (on parle alors de faille de sécurité)…
Mais… dans $N = p \times q$, $p$ et $q$ sont des entrées dérobées !

Oui ! Tout chiffrement comporte une entrée dérobée très difficile à obtenir.

Justement, les sacs à dos ! #

Le problème du sac à dos est $NP-complet$, c’est un bon candidat pour un algorithme de chiffrement !

Il fut le premier candidat (Martin Hellman, Ralph Merkle et Whitfield Diffie - 1976) pour ce rôle. Hélas aucune solution n’est fiable.

La difficulté repose dans le déchiffrement. Si le destinataire ne parvient pas à décoder, ça ne sert à rien. Il faut donc trouver un moyen de se ramener à une situation simple, où l’algorithme glouton fonctionne (poids super croissants !).

Et nous n’y sommes jamais parvenu. Chaque algorithme proposé qui résolve les 2 problèmes (difficile à décoder sans la clé, facile à décoder avec la clé) laisse derrière lui une autre porte dérobée qui rend le décodage facile pour un pirate.

qkzk

Compléments algorithmique #

Recherche dichotomique #

$x$ est-il un élément de ma $liste$ ? #

Solutions natives en Python #

solution naïve #

Recherche dichotomique #

Exercice #

Solution - pseudo code #

Solution (suite) #

Solution en python (P. Tutor) #

Algorithmes gloutons #

Les algorithmes gloutons (greedy) #

Le problème du sac à dos #

Algorithme glouton #

Sac à dos : glouton, exemple #

Est-ce le meilleur algorithme ? #

Algorithme glouton : inutile ? #

suite super croissante : #

Sac à dos : un problème fréquent #

Sac à dos : un problème $NP$-complet #

Recherche d’une solution #

Arbre binaire #

coût exponentiel #

$P = NP$ ? #

Cryptographie #

Clé publique, clé privée #

Ça sert à quelque chose tout ça ? #

Et ça fonctionne ? #

Entrée dérobée ? #

Justement, les sacs à dos ! #