pdf pour impression et diaporama
Comment stocker des informations dans une machine ? #
Une idée relativement récente #
- Machine à calculer : Antiquité
- Machine pour stocker de l’information : XVIIIeme siècle.
Historique sommaire #
En 1725 on voit l’apparition des cartes perforées : feuilles de papier rigides sur lesquelles sont disposés des trous qui symbolisent des données.
On stockait, par exemple, les plans de conception de tricot jacquard

Technologies modernes #
-
l’électromagnétisme (aimants) et de la mécanique (ça tourne): bande, cassette, disquette et disques durs pour le stockage.
-
de l’électronique pure pour la mémoire vive et la mémoire flash. $10^4$ fois plus rapide…
Mémoire vive vs mémoire morte #
- mémoire vive ou RAM : non persistante (=volatile). Perdue sans alimentation.
- mémoire morte ou ROM : persistante. Écrite une fois, ne peut qu’être lue.
- mémoire de masse : persistante. Sert au stockage. Réinscriptible.
Pourquoi utiliser la mémoire vive si on peut la perdre ? Parce que c’est plus (beaucoup) rapide !
Objectifs #
Optimiser à la fois l’espace en mémoire et les temps d’accès.

Mémoire flash #
Depuis 30 ans : mémoire flash, plus rapide, sans élément mécanique, peu gourmande en énergie mais coûteuse.


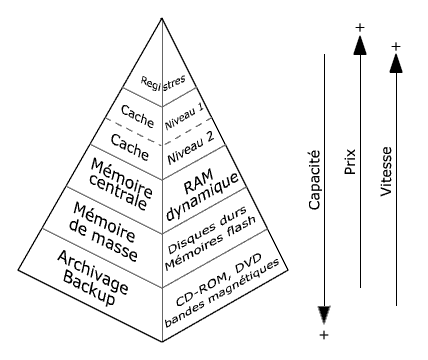
Pyramide de la mémoire #
On peut résumer ainsi :
- Rapide = coûteux = limité en espace
- Lent = économique = vaste en espace
Pyramide de la mémoire #
Nombres en informatique. #
Nous avons 10 doigts et comptons avec 10 chiffres.
En informatique on emploie un autre système pour représenter les nombres :
Les bits (0 et 1) et les octets #
1 bit : 0 ou 1. Unité minimale de symbole b, parfois bit.
1 octet : paquet de 8 bits. Symbole B (anglais pour Byte) ou o.
1 octet peut donc représenter $2^8 = 256$ valeurs distinctes.
Pourquoi deux unités ? Parce que la mémoire est lue par mots et qu’un mot est un multiple de 8 bits.
Attention aux confusions !
Données : ordre de grandeur #
| Préfixe | long | $10^n$ | Exemple |
|---|---|---|---|
| kilo | milliers | $10^3$ | $3,5$ kb = $3500$ bits |
| mega | millions | $10^6$ | $1$ Mb = 1 million de bits = 125 kB |
| giga | milliards | $10^9$ | |
| téra | billions | $10^{12}$ | $1$ TB = $8 \times 10 ^{12}$ b |
| péta | billiards | $10^{15}$ |
Quelques exemples #
| Objet | Espace mémoire |
|---|---|
| 1 lettre | 7 bits en ASCII |
| 1 page de texte | $3 \times 10^4$ bits |
| Disquette 3.5" | $1,44$ MB = $1,2 \times 10^7$ bits |
| Disque dur en 1980 | $20$ MB = $1,6 \times 10^8$ bits |
| Bdd du WDCC | $5000$ TB = $4 \times 10^{16}$ bits |
| Trafic internet (2016) | $1.56\times 10^9$ TB= $1,25 \times 10^{22}$ bits |
| 1 gramme d’ADN | $1,8 \times 10^{22}$ bits |
Pourquoi les bits de données ? #
Partons de ce qu’on sait faire :
- On sait construire de très petits transistors.
- On sait les concentrer sur une petite surface.
- L’amélioration des technologies permet de concentrer l’information et la puissance de calcul.
Par exemple :
- 1971 : 2300 transistors dans un processeur 4004.
- 2014 : 2,6 milliards dans un core i7 d’intel.
Le choix d’utiliser l’électronique pour stocker l’information est une conséquence de notre capacité à calculer avec des portes logiques.
