Correction d’un algorithme #

Afin de justifier qu’un algorithme est juste on doit s’assurer de plusieurs choses :

Qu’il termine bien.

Qu’il fait ce qu’il affirme.

Variant et invariant #

Un variant de boucle est une valeur entière positive qui décroît à chaque passage dans la boucle.

On prouve souvent la terminaison d’un algorithme en identifiant un variant de boucle.

Dans une boucle bornée (for i in range(3)) il n’est pas utile de donner un variant, par définition cette boucle termine.

Un invariant de boucle est une propriété qui est vraie au début et à la fin de chaque tour de la boucle.

On prouve souvent la correction d’un algorithme en produisant un invariant de boucle.

Correction du tri par sélection #

Considérons la fonction tri_select ci-dessous.

def plus_petit(tableau: list, indice: int) -> int:
    '''
    Renvoie l'indice du plus petit élément de tableau
    à partir de `indice`.
    '''
    mini = indice
    for k in range(indice, len(tableau)):
        if tableau[k] < tableau[mini]:
            mini = k
    return mini


def tri_select(tableau: list):
    '''
    Réalise le tri par sélection du tableau donné
    '''
    for i in range(len(tableau)):
        mini = plus_petit(tableau, i)
        tableau[i], tableau[mini] = tableau[mini], tableau[i]

Terminaison #

Lorsqu’on l’appelle avec un tableau d’objets comparables, elle réalise une boucle bornée consistant à appeler la fonction plus petit.

Dans la fonction plus petit, on réalise aussi une boucle bornée.

Aussi, ces deux algorithmes terminent bien.

Invariants de boucle #

Fonction plus_petit.

L’invariant est :

mini est l’indice du plus petit des k premiers éléments du tableau.

La propriété est vraie au départ, pour k=0.

Si la propriété est vraie quand on débute un tour de boucle, elle le reste après celui-ci.

En effet, si tableau[k] < tableau[mini], alors mini prend la valeur k et la propriété reste juste.

Quand la boucle est terminée, on a eu tableau[mini] <= tableau[k] pour tous les indices k entre indice et l’indice du dernier élément.

Donc tableau[mini] est le plus petit élément du tableau.

Fonction tri_select

L’invariant est :

les i premiers éléments sont triés et sont les plus petits éléments du tableau.

Elle est vraie au départ. Les 0 premiers éléments [] sont triés.
Elle reste vraie au tour suivant, puisqu’on ajoute le plus petit des éléments de la liste.
Attention c’est ici qu’il faut se réveiller. Au second tour… on a déjà trié le plus petit des éléments. On ajoute un nouvel élément :
- c’est le plus petit des non triés,
- il est plus grand que celui déjà présent dans la liste.
- il arrive en position 2
Donc les deux premiers éléments sont triés et sont les deux plus petits du tableau.
À chaque tour suivant, on répète ce procédé donc la propriété reste vraie.

En définitive, l’invariant de boucle prouve que la liste finale est triée.

Correction du tri par insertion #

Elle se démontre d’une manière similaire.

L’invariant de la boucle externe ne change pas : après i tours de boucle, les i premiers éléments sont triés. Par contre la boucle interne consite à insérer un élément à sa place parmi les éléments déjà triés.

L’invariant de la boucle interne est : “Après j tours” de la boucle interne, l’élément qu’on cherche à insérer est plus petits que les éléments entre j + 1 et i.

Vous pouvez vérifier que cet invariant est vrai à toutes les étapes de la boucle interne.

Complexité #

La complexité d’un algorithme est une mesure du temps qu’il va prendre à s’exécuter. En particulier on cherche une relation entre la taille des données en entrée et la durée.

Afin de rendre le calcul faisable, on réalise des simplifications.

On considère que chaque opération élémentaire (ajouter, affecter, comparer etc.) a une durée constante.

Ce n’est pas tout à fait vrai mais ça l’est suffisamment pour donner des réponses fiables.

On ne s’intéresse généralement qu’à l’odre de grandeur du nombre d’opérations réalisé.

On range généralement les algorithmes dans de grandes catégories de vitesse.

Quelles opérations compter ? #

On pourrait les compter toutes. C’est ce qui donnerait les résultats les plus précis. On pourrait aussi ne compter que celles qui interviennent dans les boucles.
Intéressons nous au nombre de comparaisons effectuées dans l’algorithme.

Complexité du tri par sélection #

def plus_petit(tableau: list, indice: int) -> int:
    '''renvoie l'indice du plus petit élément de tableau à partir de "indice"'''
    mini = indice
    for k in range(indice, len(tableau)):
        if tableau[k] < tableau[mini]:
            mini = k
    return mini


def tri_select(tableau: list) -> None:
    '''réalise le tri par sélection du tableau donné'''
    for i in range(len(tableau)):
        mini = plus_petit(tableau, i)
        tableau[i], tableau[mini] = tableau[mini], tableau[i]

Où compare-t-on ? Dans la boucle interne, en particulier, dans la fonction plus_petit.

Cette fonction réalise une boucle qui tourne de indice = 0 jusque indice = len(tableau - 1)

Notons $n$ la taille du tableau.

Regardons dans la fonction appelante tri_select : indice est ici noté i et évolue de $0$ à $n - 1$.

On fait donc, pour chaque $i$ allant de 0 à $n - 1$, à chaque fois $n - i$ comparaisons.

Notons $C$ le nombre de comparaisons. On a alors :

$$C = (n-1) + (n-2) + (n-3) + \cdots + 2 + 1$$

Qu’on réordonne par ordre croissant.

$$C = 1 + 2 + \cdots + (n-2) + (n-1)$$

Formule que vous connaissaissez bien (Cf Suites arithmétiques en mathématiques) et qui vaut $$C = \dfrac{(n-1)n}{2}$$

On reconnaît ici une expression du second degré, qu’on peut développer et simplifier :

$$C = \dfrac{1}{2}(n^2 - n)$$

Seul l’ordre de grandeur nous intéresse, pas les coefficients ni le second terme donc :

$$C \leq n^2$$

On note cela $$C = O(n^2)$$ et on dit que le tri par sélection et quadratique,

son coût (=sa complexité) se comporte comme une fonction du second degré, une fonction quadratique.

À retenir : Coût du tri par sélection #

Le coût du tri par sélection évolue avec le carré de la taille du tableau d’entrée.

Complexité du tri par insertion #

La preuve est exactement la même et le résultat similaire :

À retenir : Coût du tri par insertion #

Le coût du tri par insertion évolue avec le carré de la taille du tableau d’entrée.

Remarques finales #

Les algorithmes du tri par sélection et insertion sont assez peu efficaces.
On étudiera en terminale un algorithme de tri beaucoup plus efficace : le tri fusion.
Lorsqu’on trie des données quelconques, utiliser des comparaisons est la seule approche et alors le meilleur coût qu’on puisse obtenir est $O(n \log n)$ ce qui est beaucoup mieux que $O(n^2)$
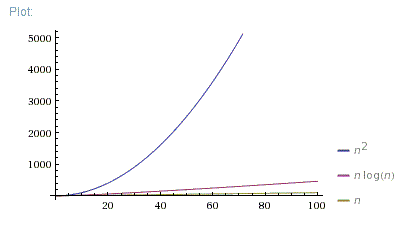
Lorsqu’on a beaucoup d’informations sur les objets à trier, on peut aller plus vite. C’est en particulier le cas lorsqu’on trie des entiers de taille limitée.
Étuder la correction et la complexité d’un algorithme sont des étapes indispensables si l’on souhaite obtenir des résultats fiables.
Tous les algorithmes ne se valent pas : s’ils sont trop lents ils ne servent à rien, s’ils sont trop difficiles à justifier, on ne peut avoir confiance en ce qu’ils font.
Cette approche, par la preuve des algorithmes, n’est pas toujours possible. On doit parfois se contenter d’une vérification empirique de leur efficacité. C’est en particulier le cas des algorithmes dits d’intelligence artificielle, comme par exemple la reconnaissance d’image ou la génération de texte.

Complexité, correction